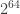
2022-8-22 09:0:0 Author: modexp.wordpress.com(查看原文) 阅读量:33 收藏
Introduction
Concise Binary Object Representation (CBOR), the binary equivalent to JavaScript Object Notation (JSON), is ideal for storing a configuration to a shellcode/stager/loader. I’ve always wanted support for text-only compression to store binary representations of ASCII strings, thus reducing the final configuration’s size while also obfuscating the contents. CBOR currently doesn’t support compression, and Zlib is recommended quite a lot for JSON, which wasn’t designed for short strings/input. A format like CBOR would benefit by supporting text-only compression, encryption and masking natively. However, in the meantime, developers are responsible for implementing those features themselves.
Huffman encoding is a lossless compression method that assigns shorter bit strings to a range of bytes. The most frequently used bytes are assigned the least amount of bits, helping reduce the size of the original input. Recovering the original data requires the same bit-to-byte mappings used during encoding. These mappings, also known as “Huffman tables”, are stored with compressed data. However, the size of these tables makes Huffman encoding unsuitable for short strings/input. LZ encoding also isn’t suitable since it works by storing full strings or a “match reference” that consists of an offset and length to the same range of bytes found earlier. Match referencing is efficient when used to compress data. However, repetition is much less likely to occur in the case of a short string. And while Zlib and LZMA are excellent compression algorithms, these are designed specifically for large data blocks rather than short strings.
In this blog post, we’ll examine how effective it is to use Base-N decoding for text-only compression. It’s similar to Huffman encoding, but without the need for Huffman tables. The results will be compared with some (but not all) of the following projects designed for compressing short strings:
- SMAZ: compression for very small strings
- shoco: a fast compressor for short strings
- Unishox2: Compression for Unicode short strings
- Skrot: A customisable compression utility dedicated to short inputs.
UniShox2 is considered the best of all and uses a combination of three encoding methods:
- Entropy coding (Huffman, Arithmetic)
- Dictionary coder (LZ77,LZ78,LZW)
- Delta encoding
Applications
In case you’re wondering why on earth compressing short strings would be useful, I’ve copied the following list of applications from the UniShox2 repository for you to consider.
- Compression for low memory devices such as Arduino and ESP8266
- Sending messages over Websockets
- Compression of Chat application text exchange including Emojis
- Storing compressed text in databases
- Faster retrieval speed when used as join keys
- Bandwidth cost saving for messages transferred to and from Cloud infrastructure
- Storage cost reduction for Cloud databases
- Some people even use it for obfuscation
Base-64 Encoding
I’ll assume most of you are familiar with Base-64 encoding, but not necessarily how it works internally. It’s a text-to-binary encoding scheme that converts 24-bits of binary to a 32-bit string. It uses 8-Bit ASCII characters to store 6-Bits of binary, which increases the data by approx. 33%. For example, encoding 32 bytes of binary would require 44 bytes of space for the encoded string. To calculate the necessary space, we divide the length of the binary by three and multiply by four. Taking into account any padding, we then align up by four. In C, we can use something like the following:
uint32_t OutLength = (((4 * (InLength / 3)) + 3) & -4).
The following is Base-64 encoding without using a lookup table.
#define ROTL32(v,n)(((v)<<(n))|((v)>>(32-(n)))) void base64_encode(void *inbuf, int inlen, char *outbuf) { uint8_t *in = (uint8_t*)inbuf; char *out = outbuf; int i; uint32_t len=0; while (inlen) { uint32_t x = 0; uint8_t c; // read 3 or less bytes. if required, pad with zeros for (len=i=0; i<3; i++) { x |= (i < inlen) ? in[len++] : 0; x <<= 8; } in += len; inlen -= len; len = (len * 8 + 4) / 6; // encode len bytes. for (i=0; i<len; i++) { x = ROTL32(x, 6); c = x % 64; if (c < 26) c += 'A'; else if (c < 52) c = (c - 26) + 'a'; else if (c < 62) c = (c - 52) + '0'; else if (c == 63) c = '+'; else c = '/'; *out++ = c; } } // if required, add padding. while (len++ < 4) *out++ = '='; *out = 0; }
Base-N Decoding
Since Base-64 encoding will increase the original data by 33%, what prevents us from using Base-64 decoding to reduce the size of arbitrary strings by 25%? We’re reversing the encoding process to compress strings into binary representations. The percentage ratio after conversion entirely depends on what characters the string contains, so you’ll get different results depending on the input. However, decoding should always result in some compression of the original string. The following table lists the approximate decrease in space used by a string when using various Base-N decoding.
| Base | Input | Alphabet | % Decrease |
|---|---|---|---|
| 2 | 64 x “0” | 01 | 88 |
| 10 | 18446744073709551615 | 0123456789 | 50 |
| 16 | FFFFFFFFFFFFFFFF | 0123456789ABCDEF | 44 |
| 26 | THEQUICKBROWNFOXJUMPSOVERTHELAZYDOG | ABCDEFGHIJKLMNOPQRSTUVWXYZ |
40 |
| 36 |
THEQUICKBROWNFOXJUMPSOVERTHELAZYDOG2 | ABCDEFGHIJKLMNOPQRSTUVWXYZ 0123456789 | 34 |
| 52 | Thequickbrownfoxjumpsoverthelazydog | ABCDEFGHIJKLMNOPQRSTUVWXYZ abcdefghijklmnopqrstuvwxyz | 29 |
| 62 | Thequickbrownfoxjumpsoverthelazydog2 | ABCDEFGHIJKLMNOPQRSTUVWXYZ abcdefghijklmnopqrstuvwxyz 0123456789 | 25 |
As you can see, a higher base number results in a lower compression ratio. And, of course, there are more printable characters required for punctuation, which will only decrease it further. My intention here isn’t to compete with or replace existing string compression tools. I’m merely pointing out that anyone can use Base-N decoding to compress strings with little effort. The following code in C can be used as a reference.
Base-N Compression with 64-Bit Integers
// // Compress string using Base-N decoding. // uint64_t base_n_compress(char str[], char base_tbl[]) { uint64_t val = 0, pwr = 1; size_t inlen = strlen(str); size_t base_n = strlen(base_tbl); for (size_t i=0; i<inlen; i++) { const char *ptr = strchr(base_tbl, str[i]); if (!ptr) return 0; int idx = (ptr - base_tbl) + 1; val += pwr * idx; pwr *= base_n; } return val; } // // Decompress string using Base-N encoding. // void base_n_decompress(uint64_t val, char base_tbl[], char str[]) { size_t base_n = strlen(base_tbl); uint64_t pwr = base_n; int outlen, i; val--; for (outlen = 1; val >= pwr; outlen++) { val -= pwr; pwr *= base_n; } str[outlen] = 0; for (i = 0; i < outlen; i++) { str[i] = base_tbl[val % base_n]; val /= base_n; } }
The only problem with this code is when the string converted to binary exceeds bits. Then we need to use bignum arithmetic. Of course, you won’t have that problem in some languages that already support multi-precision arithmetic. Getting a Python implementation of the same code without the
bits limit is relatively trivial.
Base-N Compression with Arbitrary Arithmetic
There are no limits to string compression once we start using bignum arithmetic. However, it makes more sense to use an algorithm designed specifically for large data blocks at some point. To demonstrate how it works with OpenSSL’s BIGNUM implementation. The following two functions work well for strings that might exceed bits. This code resolves the limitations of the previous code.
// // Compress a string using Base-N decoding. // void base_n_compress(BIGNUM *val, const char *str, const char *base_tbl) { size_t inlen = strlen(str); BIGNUM *pwr = BN_new(); BIGNUM *tmp = BN_new(); BIGNUM *base = BN_new(); BN_CTX *ctx = BN_CTX_new(); BN_one(pwr); // pwr = 1 BN_set_word(base, strlen(base_tbl)); // for each character for (size_t i=0; i<inlen; i++) { // get index uint8_t idx = 0; const char *ptr = strchr(base_tbl, str[i]); if (!ptr) break; idx = (uint8_t)(ptr - base_tbl) + 1; BN_set_word(tmp, idx); // BN_mul(tmp, tmp, pwr, ctx); // tmp = pwr * idx BN_add(val, val, tmp); // val += tmp BN_mul(pwr, pwr, base, ctx); // pwr *= base } BN_free(pwr); BN_free(tmp); BN_free(base); BN_CTX_free(ctx); } // // Decompress a string using Base-N encoding. // std::string base_n_decompress(BIGNUM *val, char *alpha) { const char *base_tbl = alpha; size_t outlen; std::string str; BIGNUM *pwr = BN_new(); BIGNUM *base = BN_new(); BIGNUM *rem = BN_new(); BN_CTX *ctx = BN_CTX_new(); BN_sub_word(val, 1); // val--; BN_set_word(pwr, strlen(base_tbl)); // pwr = strlen(base_tbl) BN_set_word(base, strlen(base_tbl)); // base = strlen(base_tbl) // obtain the length of string for (outlen=1; BN_cmp(val, pwr) >= 0; outlen++) { BN_sub(val, val, pwr); // val -= pwr; BN_mul(pwr, pwr, base, ctx); // pwr *= base } // write string to buffer for (size_t i=0; i<outlen; i++) { BN_div(val, rem, val, base, ctx); // val % tbl_len unsigned long r = BN_get_word(rem); str.push_back(base_tbl[r]); } BN_free(pwr); BN_free(rem); BN_free(base); BN_CTX_free(ctx); return str; }
Frequency Analysis
Base-N decoding doesn’t choose the length of bit strings optimally. It doesn’t assign the shortest amount of bits to bytes that occur more frequently in the string like Huffman encoding. If we only use a base number equivalent to the length of unique characters in the string, we can compress it even better. The following code can generate an optimal alphabet based on the string to compress.
// // Generate an alphabet for optimal compression. // void generate_alphabet(char *alpha, std::string str) { std::unordered_map<char, int> freq; // count frequency of each character in string we want to compress. for (const char &c: str) { freq[c]++; } // convert map to a vector and sort in ascending order. std::vector<std::pair<char, int>> elems(freq.begin(), freq.end()); std::sort(elems.begin(), elems.end(), [](auto &left, auto &right) { return left.second > right.second; }); // save each character to output buffer. for (auto &pair : elems) { *alpha++ = pair.first; } }
We perform the same tests as before and see a distinct improvement. However, the higher compression ratio is more likely the result of a smaller lookup table/base number rather than sorting the most frequent characters in ascending order.
| Base | Input | Alphabet | % Decrease |
|---|---|---|---|
| 1 | 64 x “0” | 0 | 99 |
| 9 | 18446744073709551615 | 457106938 | 60 |
| 1 | FFFFFFFFFFFFFFFF | f | 94 |
| 26 | THEQUICKBROWNFOXJUMPSOVERTHELAZYDOG | OERUHTNGWBKCIQFXJMPSVLAZYD |
40 |
| 27 |
THEQUICKBROWNFOXJUMPSOVERTHELAZYDOG2 | OERUTHNGW2BKCIQFXJMPSVLAZYD | 39 |
| 27 | Thequickbrownfoxjumpsoverthelazydog | oeruhfwbkciqTngxjmpsvtlazyd | 40 |
| 28 | Thequickbrownfoxjumpsoverthelazydog2 | oeruhfwbkciqTngxjmpsvtl2azyd | 39 |
Compared to Other Libraries
The following examples are from the UniShox2 repository. Green columns highlight the best ratio, but these are only preliminary tests. The Base-N decoding uses frequency analysis before compression. I would not want to claim that Base-N compression outperforms UniShox2!
| String | Size | UniShox2 | Base-N Decoding |
Shoco |
|---|---|---|---|---|
| Beauty is not in the face. Beauty is a light in the heart. | 58 | 30 | 31 |
46 |
| The quick brown fox jumps over the lazy dog. | 44 | 31 | 27 | 38 |
| WRITING ENTIRELY IN BLOCK CAPITALS IS SHOUTING, and it’s rude | 61 | 47 | 38 | 58 |
| Rose is a rose is a rose is a rose. | 35 | 12 | 14 | 25 |
| 039f7094-83e4-4d7f-aa38-8844c67bd82d | 36 | 18 | 18 | 36 |
| 2021-07-15T16:37:35.897Z | 24 | 9 | 12 |
24 |
| (760) 756-7568 | 14 | 7 | 6 | 14 |
| This is a loooooooooooooooooooooong string | 42 | 15 | 19 | 25 |
Summary
We see that Base-N decoding, which works similar to Huffman encoding, can be effective for compressing and obfuscating short strings. The results are even better when frequency analysis occurs before compression. Shuffling the bits used in the base table makes it possible to have a type of “polymorphic text-to-binary” algorithm. There are limitations, of course, like the need for multi-precision arithmetic when the conversion of string to binary exceeds or
bit integers. However, perhaps someone will devise a more optimal algorithm that avoids the need for such.
如有侵权请联系:admin#unsafe.sh