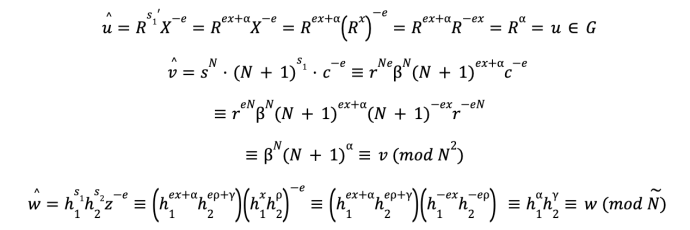Specialized Zero-Knowledge Proof failures

By Opal Wright

Zero-knowledge (ZK) proofs are useful cryptographic tools that have seen an explosion of interest in recent years, largely due to their applications to cryptocurrency. The fundamental idea of a ZK proof is that a person with a secret piece of information (a cryptographic key, for instance) can prove something about the secret without revealing the secret itself. Cryptocurrencies are using ZK proofs for all sorts of fun things right now, including anonymity, transaction privacy, and “roll-up” systems that help increase the efficiency of blockchains by using ZK proofs to batch transactions together. ZK proofs are also being used in more general ways, such as allowing security researchers to prove that they know how to exploit a software bug without revealing information about the bug.

As with most things in cryptography, though, it’s hard to get everything right. This blog post is all about a pair of bugs in some special-purpose ZKP code that allow ne’er-do-wells to trick some popular software into accepting invalid proofs of impossible statements. That includes “proving” the validity of invalid inputs to a group signature. This, in turn, can lead to invalid signatures. In blockchain systems that use threshold signatures, like ThorChain and Binance, this could allow an attacker to prevent targeted transactions from completing, creating a denial-of-service attack– against the chain as a whole or against specific participants.

Background on discrete log proofs

One specialized ZK proof is a discrete logarithm proof of knowledge. Suppose Bob provides Alice with an RSA modulus N = PQ, where P and Q are very large primes known only to Bob, and Bob wants to prove to Alice that he knows a secret exponent x such that s ≡ t^x (mod N). That is, x is the discrete logarithm of s with respect to base t, and he wants to prove that he knows x without revealing anything about it.

The protocol works as follows:

First, Bob and Alice agree on a security parameter k, which is a positive integer that determines how many iterations of the protocol to perform. In practice, this is usually set to k = 128.
Second, Bob randomly samples a_i from Z_Φ(N) for i=1,2,…,k, computes corresponding values α_i = t^a_i (mod N), and sends α1,α2,…,α_k to Alice.
Third, Alice responds with a sequence of random bits c₁,c₂,…,c_k.
Fourth, Bob computes z_i = a_i + c_ix and sends z₁,z₂,…,z_k to Alice.
Finally, Alice checks that t^z_i ≡ α_is^c_i (mod N) for all i = 1,2,…,k. If all the checks pass, she accepts the proof and is confident that Bob really knows x. Otherwise, she rejects the proof—Bob may be cheating!

Why it works

Suppose Bob doesn’t know x. For each i, Bob has two ways to attempt to fool Alice: one if he thinks Alice will pick c_i = 0, and one if he thinks Alice will pick c_i = 1.

If Bob guesses that Alice will select c_i = 0, he can select a random a_i ∈ Z_N and send Alice α_i = t^a_i mod N. If Alice selects c_i = 0, Bob sends Alice z_i = a_i, and Alice sees that t^z_i ≡ t^a_i ≡ α_is⁰ ≡ α_i (mod N) and accepts the i-th iteration of the proof. On the other hand, if Alice selects c_i = 1, Bob needs to compute z_i such that t^z_i ≡ t^a_is (mod N). That is, he needs to find the discrete logarithm of t^a_is, which is equal to a_i + x. However, Bob doesn’t know x, so he can’t compute a z_i that will pass Alice’s check.

On the other hand, if Bob guesses that Alice will select c_i = 0, he can select a random a_i ∈ Z_N and send Alice α_i = t^a_is⁻¹ (mod N). If Alice selects c_i = 1, Bob sends Alice z_i = a_i. Alice sees that t^z_i ≡ t^a_i and t^a_i≡ α_is ≡ t^α_is⁻¹s ≡ t^a_i (mod N), and accepts the i-th iteration of the proof. But if Alice selects c_i = 0, Bob needs to compute z_i such that t^z_i ≡ t^a_is⁻¹ (mod N), which would be z_i = a_i − x. But again, since Bob doesn’t know x, he can’t compute a z_i that will pass Alice’s check.

The trick is, each of Bob’s guesses only has a 50 percent chance of being right. If any one of Bob’s k guesses for Alice’s c_i values are wrong, Alice will reject the proof as invalid. If Alice is choosing her c_i values randomly, that means Bob’s chances of fooling Alice are about 1 in 2^k.

Typically, Alice and Bob will use parameters like k = 128. Bob has a better chance of hitting the Powerball jackpot four times in a row than he does of guessing all c1,c2,…,c128 correctly.

In the case of a non-interactive proof, as we’ll see in the code below, we don’t rely on Alice to pick the values c_i. Instead, Bob and Alice each compute a hash of all the values relevant to the proof: c = Hash(N ∥ s ∥ t ∥ α₁ ∥ … ∥ α_k). The bits of c are used as the c_i values. This is called the Fiat-Shamir transform. It’s certainly possible to get the Fiat-Shamir transform wrong, with some pretty nasty consequences, but the bugs discussed in this article will not involve Fiat-Shamir failures.

The code

Our proof structure and verification code come from tss-lib, written by the folks at Binance. We came across this code while reviewing other software, and the Binance folks were super responsive when we flagged this issue for them.

To start with, we have our Proof structure:

type (
    Proof struct {
        Alpha,
        T [Iterations]*big.Int
    }
)

This is a fairly straightforward structure. We have two arrays of large integers, Alpha and T. These correspond, respectively, to the α_i and z_i values in the mathematical description above. It’s notable that the Proof structure does not incorporate the modulus N or the values s and t.

func (p *Proof) Verify(h1, h2, N *big.Int) bool {
    if p == nil {
        return false
    }
    modN := common.ModInt(N)
    msg := append([]*big.Int{h1, h2, N}, p.Alpha[:]...)
    c := common.SHA512_256i(msg...)
    cIBI := new(big.Int)
    for i := 0; i < Iterations; i++ {
        if p.Alpha[i] == nil || p.T[i] == nil {
            return false
        }
        cI := c.Bit(i)
        cIBI = cIBI.SetInt64(int64(cI))
        h1ExpTi := modN.Exp(h1, p.T[i])
        h2ExpCi := modN.Exp(h2, cIBI)
        alphaIMulH2ExpCi := modN.Mul(p.Alpha[i], h2ExpCi)
        if h1ExpTi.Cmp(alphaIMulH2ExpCi) != 0 {
            return false
        }
    }
    return true
}

This code actually implements the verification algorithm. The arguments h1 and h2 correspond to t and s, respectively. First, it computes the challenge value c. Then, for each bit c_i of c, it computes:

If h1ExpTi ≠ alphaIMulH2ExpCi for any 0 < i ≤ k, the proof is rejected. Otherwise, it is accepted.

The issue

The thing to notice is that the Verify function doesn’t do any sort of check to validate h1, h2, or any of the elements of p.Alpha or p.T. A lack of validity checks means we can trigger all sorts of fun edge cases. In particular, when it comes to logarithms and exponential relationships, it’s important to look out for zero. Recall that, for any x ≠ 0, we have 0^x = 0. Additionally, for any x, we have 0 ∙ x = 0. We are going to exploit these facts to force the equality check h1ExpTi = alphaIMulH2ExpCi to always pass.

The first impossible thing: Base-0 Discrete Logs

Suppose Bob creates a Proof structure p with the following values:

All elements of p.T are positive (that is, z_i > 0 for all i)
All elements of p.Alpha are set to 0 (that is, α_i = 0 for all i)

Now consider a call to the Verify function with the following parameters:

N is the product of two large primes
h1 set to any integer (that is, s is unconstrained)
h2 set to 0 (that is, t = 0)

The Verify function will check that t^z_i ≡ α_is^c_i (mod N). On the right hand side of the relationship, α_i = 0 forces α_is^c_i= 0. On the left hand side of the equation, t^z_i = 0^z_i = 0 because z_i > 0. Thus, the Verify function sees that 0 = 0, and accepts the proof as valid. Recall that the proof is meant to demonstrate that Bob knows the discrete log of s with respect to t. In this case, the Verifier routine will believe that Bob knows an integer x such that s ≡ 0^x (mod N) for any s. But if s ∉ {0,1}, that’s impossible!

The fix

Preventing this problem is straightforward: validate that h2 and the elements of p.Alpha are all non-zero. As a matter of practice, it is a good idea to validate all cryptographic values provided by another party, ensuring that, for example, elliptic curve points lie on a curve and that integers fall within their appropriate intervals and satisfy any multiplicative properties. In the case of this proof, such validation would include checking that h1, h2, and p.Alpha are non-zero, relatively prime to N, and fall within the interval [1,N). It would also be a good idea to ensure that N passes some basic checks (such as a bit length check).

Proof of encryption of a discrete log

In some threshold signature protocols, one of the steps in the signature process involves proving two things simultaneously about a secret integer x that Bob knows:

That X = R^x, where X and R are in an order-q group G (typically, G will be the multiplicative group of integers for some modulus, or an elliptic curve group)
That a ciphertext c = PaillierEnc_N(x,r) for some randomization value r ∈ Z^⋆_N and Bob’s public key N. That is, c = (N + 1)^xr^N (mod N²).

(Just for clarity: G is typically specified alongside a maximal-order group generator g ∈ G. It doesn’t get used directly in the protocol, but it does get integrated into a hash calculation – it doesn’t affect the proof, so don’t worry about it too much.)

Proving this consistency between the ciphertext c and the discrete logarithm of X ensures that Bob’s contribution to an elliptic curve signature is the same value he contributed at an earlier point in the protocol. This prevents Bob from contributing bogus X values that lead to invalid signatures.

As part of the key generation, a set of “proof parameters” are generated, including a semiprime modulus Ñ (whose factorization is unknown to Alice and Bob), as well as h₁ and h₂, both coprime to Ñ.

Bob begins by selecting uniform random values α←^$Z_q³,β←^$Z^*_N,γ←^$Z_q^3Ñ and ρ←^$Z_q^3Ñ.

Bob then computes:

Finally, Bob computes a Fiat-Shamir challenge value e = Hash(N,Ñ,h₁,h₂,g,q,R,X,c,u,z,v,w) and the challenge response values:

Note that s₁ and s₂ are computed not modulo any value, but over the integers. Bob then sends Alice the proof π_PDL=[z,e,s,s₁,s₂].

Alice, upon receiving π_PDL, first checks that s₁ ≤ q³; if this check fails, she rejects the proof as invalid. She then computes:

Finally, Alice computes:

If e ≠ ê, she rejects <π_PDL as invalid. Otherwise, she accepts π_PDL as valid.

Why it works

First, let’s make sure that a valid proof will validate:

Because u (with a hat), v (with a hat) and w (with a hat), match u, v, and w (respectively), we will have ê, = e, and the proof will validate.

To understand how Bob is prevented from cheating, read this paper and section 6 of this paper.

The code

The following code is taken from the kryptology library’s Paillier discrete log proof implementation. Specifically, the following code is used to compute v (with a hat):

func (p PdlProof) vHatConstruct(pv *PdlVerifyParams) (*big.Int, error) {
    // 5. \hat{v} = s^N . (N + 1)^s_1 . c^-e mod N^2

    // s^N . (N + 1)^s_1 mod N^2
    pedersenInc, err := inc(p.s1, p.s, pv.Pk.N)
    if err != nil {
        return nil, err
    }

    cInv, err := crypto.Inv(pv.C, pv.Pk.N2)
    if err != nil {
        return nil, err
    }
    cInvToE := new(big.Int).Exp(cInv, p.e, pv.Pk.N2)
    vHat, err := crypto.Mul(pedersenInc, cInvToE, pv.Pk.N2)
    if err != nil {
        return nil, err
    }
    return vHat, nil
}

The calling function, Verify, uses vHatConstruct to compute the v (with a hat) value described above. In a valid proof, everything should work out just fine.

The issue

In an invalid proof, things do not work out just fine. In particular, it is possible for Bob to set v = s = 0 . When this happens, the value of c is irrelevant: Alice winds up checking that v (with a hat) = 0^N ∙ (N+1)_{s₁ ∙ c^−e = 0 = v}, and accepts the result.

The second impossible thing: Arbitrary Ciphertexts

By exploiting the v (with a hat) = s = 0 issue, Bob can prove that he knows x such that X = R^x, but simultaneously “prove” to Alice that any value for c ≠ 0 is a valid ciphertext for x. Bob doesn’t even need to know the factorization of N. Once again, Bob has “proved” the impossible!

This forgery has real security implications. In particular, being able to forge this proof allows Bob to sabotage the threshold signature protocol without being detected. In some systems, this could be used to prevent valid transactions from being performed.

It is worth noting: the specific case of c = 0 will be detected as an error. The line cInv, err := crypto.Inv(pv.C, pv.Pk.N2) attempts to invert c modulo N². When c = 0, this function will return an error, causing the vHatConstruct function to return an error in turn.

The fix

Again, this can be prevented by better input validation. Basic validation of the proof would involve checking that z and s are in Z^*_N. That is, checking that gcd(z,N) = gcd(s,N) = 1, which forces z ≠ 0 and s ≠ 0. Additionally, there should be checks to ensure s₁ ≠ 0 and s₂ ≠ 0.

Risks and disclosure

The risk

These bugs were found in repositories that implement the GG20 threshold signature scheme. If attackers exploit the ciphertext malleability bug, they can “prove” the validity of invalid inputs to a group signature, leading to invalid signatures. If a particular blockchain relies on threshold signatures, this could allow an attacker to prevent targeted transactions from completing.

Disclosure

We have reported the issues with tss-lib to Binance, who promptly fixed them. We have also reached out to numerous projects that rely on tss-lib (or, more commonly, forks of tss-lib). This includes ThorChain, who have also fixed the code; Joltify and SwipeChain rely directly on the ThorChain fork. Additionally, Keep Networks maintains their own fork of tss-lib; they have integrated fixes.

The issue with kryptology has been reported to Coinbase. The kryptology project on GitHub has since been archived. We were not able to identify any current projects that rely on the library’s threshold signature implementation.

The moral of the story

In the end, this is a cryptographic failure stemming from a completely understandable data validation oversight. Values provided by another party should always be checked against all applicable constraints before being used. Heck, values computed from values provided by another party should always be checked against all applicable constraints.

But if you look at mathematical descriptions of these ZK proofs, or even well-written pseudocode, where are these constraints spelled out? These documents describe the algorithms mathematically, not concretely. You see steps such as β←^$Z^*_N, followed later by v = (N + 1)^αβ^N (mod N²). From a mathematical standpoint, it’s understood that v is in Z^*_N², and thus v ≠ 0. From a programming standpoint, though, there’s no explicit indication that there’s a constraint to check on v.

Trail of Bits maintains a resource guide for ZK proof systems at zkdocs.com. These types of issues are one of our primary motivations for such guidance—translating mathematical and theoretical descriptions into software is a difficult process. Admittedly, some of our own descriptions could explain these checks more clearly; we’re hoping to have that fixed in an upcoming release.

One piece of guidance that Trail of Bits likes to give auditors and cryptographers is to look out for two special values: 0 and 1 (as well as their analogues, like the point at infinity). Bugs related to 0 or its analogues have caused problems in the past (for instance, here and here). In this case, a failure to check for 0 leads to two separate bugs that allow attackers in a threshold signature scheme to lead honest parties down a rabbit hole.