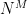PRFs, PRPs and other fantastic things

A few weeks ago I ran into a conversation on Twitter about the weaknesses of applied cryptography textbooks, and how they tend to spend way too much time lecturing people about Feistel networks and the boring details of AES. Some of the folks in this conversation suggested that instead of these things, we should be digging into more fundamental topics like “what is a pseudorandom function.” (I’d link to the thread itself, but today’s Twitter is basically a forgetting machine.)

This particular point struck a chord with me. While I don’t grant the premise that Feistel networks are useless, it is true that pseudorandom functions, also known as PRFs, are awfully fundamental. Moreover: these are concepts that get way too little coverage in (non-theory) texts. Since that seems bad for aspiring practitioners, I figured I’d spend a little time trying to explain these concepts in an intuitive way — in the hopes that I can bring the useful parts to folks who aren’t being exposed to these ideas directly.

This is going to be a high-level post and hence it will skip all the useful formalism. It’s also a little wonky, so feel free to skip it if you don’t really care. Also: since I need to be contrary: I’m going to talk about Feistel networks anyway. That bit will come later.

What’s a PRF, and why should I care?

Pseudorandom functions (PRFs) and pseudorandom permutations (PRPs) are two of the most fundamental primitives in modern cryptography. If you’ve ever implemented any cryptography yourself, there’s an excellent chance you relied on an algorithm like AES, HMAC or ChaCha20 to implement either encryption or authentication. If you did this, then you probably relied on some security property you assumed those primitives to have. But what precisely is that security property you’re relying on?

We could re-imagine this security definition from scratch every time we look at a new cipher. Alternatively, we could start from a much smaller number of general mathematical objects that provide security properties that we can reason about, and try to compare those to the algorithms we actually use. The second approach has a major advantage: it’s very modular. That is, rather than re-design every single protocol each time we come up it with a new type of cipher, all we really need to do is to analyze it with the idealized mathematical objects. Then we can realize it using actual ciphers, which hopefully satisfy these well-known properties.

Two of the most common such objects are the pseudorandom function (PRF) and the pseudorandom permutation (PRP). At the highest level, these functions have two critical properties that are extremely important to cryptographers:

They are keyed functions: this means that they take in a secret key as well as some input value. (This distinguishes them from some hash functions.)
The output of a PRF (or PRP), when evaluated on some unique input, typically appears “random.” (But explaining this rough intuition precisely will require some finesse, see below.)

If a function actually can truly achieve those properties, we can use it to accomplish a variety of useful tasks. At the barest minimum, these properties let us accomplish message authentication (by building MACs), symmetric encryption by building stream ciphers, and key derivation (or “pluralization”) in which a single key is turned into many distinct keys. We can also use PRFs and PRPs to build other, more fundamental primitives such as pseudorandom number generators and modes of operation, which happen to be useful when encrypting things with block ciphers.

The how and why is a little complex, and that’s the part that will require all the explanation.

Random functions

There are many ideal primitives we’d love to be able to use in cryptography, but are thwarted from using due to the fact that they’re inefficient. One of the most useful of these is the random function.

Computer programmers tend to get confused about functions. This is mostly because programming language designers have convinced us that functions are the same thing as the subroutines (algorithms) that we use to compute them. In the purely mathematical sense, it’s much more useful to forget about algorithms, and instead think of functions as simply being a mapping from some set of input values (the domain) to some set of output values (the range).

If we must think about implementing functions, then for any function with a finite domain and range, there is always a simple way to implement it: simply draw up a giant (and yet still finite!) lookup table that contains the mapping from each input to the appropriate output value. Given such a table, you can always quickly realize an algorithm for evaluating it, simply by hard-coding the table into your software and performing a table lookup. (We obviously try not to do this when implementing software — indeed, most of applied computer science can be summarized as “finding ways to avoid using giant lookup tables”.)

A nice thing about the lookup table description of functions is that it helps us reason about concepts like the number of possible functions that can exist for a specific domain and range. Concretely: if a function has M distinct input values and N outputs, then the number of distinct functions sharing that profile is $N^M$ . This probably won’t scale very well for even modest values of M and N, but let’s put this aside for a moment. Given enough paper, we could imagine writing down each unique lookup table on a piece of paper: then we could stack those papers up and admire the minor ecological disaster we’d have just created.

Now let’s take this thought-experiment one step farther: imagine that we could walk out among those huge stacks of paper we’ll have just created, and somehow pick one of these unique lookup tables uniformly at random. If we could perform this trick routinely, the result would be a true “random function”, and it would make an excellent primitive to use for cryptography. We could use these random functions to build hash functions, stream ciphers and all sorts of other things that would make our lives much easier.

There are some problems with this thought experiment, however.

A big problem is that, for functions with non-trivial domain and range, there just isn’t enough paper in the world to enumerate every possible function. Even toy examples fall apart quickly. Consider a tiny hash function that takes in (and outputs) only 4-bit strings. This gives us M=16 inputs and N=16 outputs, and hence number of (distinct) mappings is $16^{16} = 2^{64}$ , or about 18 quintillion. It gets worse if you think about “useful” cryptographic functions, say those with the input/output profile of ChaCha20, which has 128-bit inputs and 512-bit outputs. There you’d need a whopping $(2^{512})^{2^{128}}$ (giant) pieces of paper. Since there are only around $2^{272}$ atoms in the observable universe (according to literally the first Google search I ran on the topic), we would quickly run into shortages even if we were somehow able to inscribe each table onto a single atom.

Obviously this version of the thought experiment is pretty silly. After all: why bother to enumerate every possible function if we’re going to throw most of them away? It would be much more efficient if we could sample a single random function directly without all the overhead.

This also turns out to be fairly straightforward: we can write down a single lookup table with M rows (corresponding to all possible inputs); for each row, we can sample a random output from the set of N possible outputs. The resulting table will be M rows long and each row will contain $log_2(N)$ bits of data.

While this seems like a huge improvement over the previous approach, it’s still not entirely kosher. Even a single lookup table is still going to huge — at least as large as the function’s entire domain. For example: if we wanted to sample a random function with the input/output profile of ChaCha20, the table would require enough paper to contain $512*2^{128} = 2^{137}$ bits.

And no, we are not going to be able to compress this table! It should be obvious now that a random function generated this way is basically just a file full of random data. Since it has maximal entropy, compression simply won’t work.

The fact that random functions aren’t efficient for doing cryptography does not always stop cryptographers from pretending that we might use them, most famously as a way to model cryptographic hash functions in our security proofs. We have an entire paradigm called the random oracle model that makes exactly this assumption. Unfortunately, in reality we can’t actually use random functions to implement cryptographic functions — sampling them, evaluating them and distributing their code are all fundamentally infeasible operations. Instead we “instantiate” our schemes with an efficient hash algorithm like SHA3, and then we pray.

However, there is one important caveat. While we generally cannot sample and share large random functions in practice, we hope we can do something almost as interesting. That is, we can build functions that appear to be random: and we can do this in a very powerful cryptographic sense.

Pseudorandom functions

Random functions represent a single function drawn from a family of functions, namely the family that consists of every possible function that has the appropriate domain and range. As noted above, the cost of this decision is that such functions cannot be sampled, evaluated or distributed efficiently.

Pseudorandom functions share a similar story to random functions. That is, they represent a single function sampled from a family. What’s different in this case is that the pseudorandom function family is vastly smaller. A benefit of this tradeoff is that we can demand that the description of the function (and its family) be compact: pseudorandom function families must possess a relatively short description, and it must be possible to both sample and evaluate them efficiently: meaning, in polynomial time.

Compared to the set of all possible functions over a given domain and range, a pseudorandom function family is positively tiny.

Let’s stick with the example of ChaCha20. As previously discussed, ChaCha has a 128-bit input, but it also takes in a 256-bit secret key. If we were to view ChaCha20 as a pseudorandom function family, then we could view it as a family of $2^{256}$ individual functions, where each key value selects exactly one function from the family.

Now let’s be clear: $2^{256}$ is still a really big number! However: it is vastly smaller than $(2^{512})^{2^{128}}$ , which is the total number of possible functions with ChaCha20’s input profile. Sampling a random 256-bit key and sharing it with to Bob is eminently feasible; indeed, your browser did something like this when you loaded this website. Sampling a “key” of bit-length ${512}*{2^{128}}$ is not.

This leaves us with an important question, however. Since ChaCha20’s key is vastly smaller than the description of a random function, and the algorithmic description of ChaCha20 is also much smaller than the description of even a single random function, is it possible for small-key function family like “ChaCha20” to be as good (for cryptographic purposes) as a true random function? And what does “good” even mean here?

Defining pseudorandomness

Mirriam-Webster defines the prefix pseudo as “being apparently rather than actually as stated.” The Urban Dictionary is more colorful: it defines pseudo as “false; not real; fake replication; bootleg; tomfoolery“, and also strongly hints that pseudo may be shorthand for pseudoephedrine (note: it is not.)

Clearly if we can describe a function using a compact algorithmic description and a compact key, then it cannot be a true random function: it is therefore bootleg. However that doesn’t mean it’s entirely tomfoolery. What pseudorandom means, in a cryptographic sense, is that a function of this form will be indistinguishable from a truly random function — at least to an adversary who does not know which function we have chosen from the family, and who has a limited amount of computing power.

Let’s unpack this definition a bit!

Imagine that I create a black box that contains one of two possible items, chosen with equal probability. Item (1) is an instance of a single function sampled at random from a purported pseudorandom function family; item (2) is a true random function sampled from the set of all possible functions. Both functions have exactly the same input/output profile, meaning they take in inputs of the same length, and produce outputs of the same length (here we are excluding the key.)

Now imagine that I give you “oracle” access to this box. What this means is: you will be allowed to submit any input values you want, and the box will evaluate your input using whichever function it contains. You will only see the output. (And no, you don’t get to time the box or measure any side channels it might compute, this is a thought experiment.) You can submit as many inputs as you want, using any strategy for choosing them that you desire: they simply have to be valid inputs, meaning that they’re within the domain of the function. We will further stipulate that you will be computationally limited: that means you will only be able to compute for a limited (polynomial in, say, the PRF’s key length) number of timesteps. At the end of the day, your goal is to guess which type of function I’ve placed in the box.

We say that a family of functions is pseudorandom if for every possible efficient strategy (meaning, using any algorithm that runs in time polynomial in the key size, provided these algorithms were enumerated before the function was sampled), the “advantage” you will have in guessing what’s in the box is very tiny (at most negligible in, say, the size of the function’s key.)

A fundamental requirement of this definition is that the PRF’s key/seed (aka the selector that chooses which function to use) has to remain secret from the adversary. This is because the description of the PRF family itself cannot be kept secret: that is both good cryptographic practice (known as Kerckhoff’s principle), but also due to the way we’ve defined the problem over “all possible algorithms”, which necessarily includes algorithms that have the PRF family’s description coded inside of them.

And pseudorandom functions cannot possibly be indistinguishable from random ones if the attacker can learn or guess the PRF’s secret key: this would allow the adversary to simply compute the function themselves and compare the results they get to the values that come out of the oracle (thus winning the experiment nearly 100% of the time.)

There’s a corollary to this observation: since the key length of the PRF is relatively short, the pseudorandomness guarantee can only be computational in nature. For example, imagine the key is 256 bits long: an attacker with unlimited computational resources could brute-force guess its way through all possible 256-bit keys and test each one against the results coming from the oracle. If the box truly contains a PRF, then with high probability she’ll eventually find a key that produces the same results as what comes out of the box; if the box contains a random function, then she probably won’t. To rule such attacks out of bounds we must assume that the adversary is not powerful enough to test a large fraction of the keyspace. (In practice this requirement is pretty reasonable, since brute forcing through an n-bit keyspace requires on the order of $2^n$ work, and we assume that there exist reasonable values of n for which no computing device exists that can succeed at this.)

So what can we do with pseudorandom functions?

As I mentioned above, pseudorandom functions are extremely useful for a number of basic cryptographic purposes. Let’s give a handful here.

Building stream ciphers. One of the simplest applications of a PRF is to use it to build an efficient stream cipher. Indeed, this is exactly what the ChaCha20 function is typically used for. Let us assume for the moment that ChaCha20 is a PRF family (I’ll come back to this assumption later.) Then we could select a random key and evaluate the function on a series of unique input values — the ChaCha20 IETF proposals suggest concatenating a 64-bit block number with a counter — and then concatenate the outputs of the function together to produce a keystream of bits. To encrypt a message we would simply exclusive-OR (XOR) this string of bits (called a “keystream”) with the message to be enciphered.

Why is this reasonable? The argument breaks down into three steps:

If we had generated the keystream using a perfect random number generator (and kept it secret, and never re-used the keystream) then the result would be a one-time pad, which is known to be perfectly secure.
And indeed, had we had been computing this output using a truly random function (with a ChaCha20-like I/O profile) where each input was used exactly once, the result of this evaluation would indeed have been such a random string.
Of course we didn’t do this: we used a PRF. But here we can rely on the fact that our attackers cannot distinguish PRF output from that of a random function.

One can make the last argument the other way around, too. If our attacker is much better at “breaking” the stream cipher implemented with a PRF than they are at breaking one implemented with a random function, then they are implicitly “distinguishing” the two types of function with a substantial advantage — and this is precisely what the definition of a PRF says that an attacker cannot do!

Constructing MACs. A PRF with a sufficiently large range can also be used as a Message Authentication Code. Given a message M, the output of PRF(k, M) — the PRF evaluated on a secret key k and the message M — should itself be indistinguishable from the output of a random function. Since this output will effectively be a random string, this means that an attacker who has not previously seen a MAC on M should have a hard time guessing the appropriate MAC for a given message. (The “strength” of the MAC will be proportional to the output length of the PRF.)

Key derivation. Often in cryptography we have a single random key k and we need to turn this into several random-looking keys (k1, k2, etc.) This happens within protocols like TLS, which (at least in version 1.3) has an entire tree of keys that it derives from a single master secret. PRFs, it turns out, are an excellent for this task. To “diversify” a single key into multiple keys, one can simply evaluate the PRF at a series of distinct points (say, k1 = PRF(k, 1), k2 = PRF(k, 2), and so on), and the result is a set of keys that are indistinguishable from random; provided that the PRF does what it says it does.

There are, of course, many other applications for PRFs; but these are some pretty important ones.

Pseudorandom permutations

Up until now we’ve talked about pseudorandom functions (PRFs): these are functions that have output that is indistinguishable from a random function. A related concept is that of the pseudorandom permutation (PRP). Pseudorandom permutations share many of the essential properties of PRFs, with one crucial difference: these functions realize a permutation of their input space. That is: if we concentrate on a given function in the family (or, translating to practical terms, we fix one “key”) then each distinct input maps to a distinct output (and vice versa.)

A nice feature of permutations is that they are potentially invertible, which makes them a useful model for something we use very often in cryptography: block ciphers. These ciphers take in a key and a plaintext string, and output a ciphertext of the same length as the plaintext. Most critically, this ciphertext can be deciphered back to the original plaintext. Note that a standard (pseudo)random function doesn’t necessarily allow this: for example, a PRF instance F can map multiple inputs (A, B) such that F(A) = F(B), which makes it very hard to uniquely invert either output.

The definition of a pseudorandom permutation is very similar to that of a PRF: they must be indistinguishable from some idealized function — only in this case the ideal object is a random permutation. A random permutation is simply a function sampled uniformly from the set of all possible permutations over the domain and range. (Because really, why wouldn’t it be?)

There are two important mathematical features of PRPs that I should mention here:

PRPs are actually PRFs (to an extent.) A well-known result in cryptography, called the “PRP/PRF switching lemma” demonstrates that a PRP with sufficiently-large domain and range basically “is” a PRF. Put differently: a pseudorandom permutation placed into an oracle can be computationally indistinguishable from an oracle that contains a random function (with the same domain and range), provided the range of the function is large enough and the attacker doesn’t make too many queries.

The intuition behind this result is fairly straightforward. If we consider this from the perspective of an attacker interacting with some function in an oracle, the only difference between a random permutation and a random function is that the former will never produce any collisions — distinct inputs that produce the same output — while the latter may (occasionally) do so.

From the adversary’s perspective, therefore, the ability to distinguish whether the oracle contains a random permutation or a random function devolves to querying the oracle to see if one can observe such a collision. Clearly if it sees even one collision of the form F(A) = F(B), then it’s not dealing with a permutation. But it may take many queries for the attacker to find such a collision in a random function, or to be confident one should already have occurred (and hence it is probably interacting with a PRP.)

In general the ability to distinguish the two is a function of the number of queries the attacker is allowed to make, as well as the size of the function’s range. After a single query, the probability of a collision (on a random function) is zero: hence the attacker has no certainty at all. After two queries, the probability is equal to 1/N where N is the number of possible outputs. As the attacker makes more queries this probability increases. Following the birthday argument the expected probability reaches p=0.5 after about $\sqrt{N}$ queries. For functions like AES, which has output size $2^{128}$ , this will occur around $2^{64}$ queries.

PRFs can be used to build PRPs. The above result shows us that PRPs are usually good enough to serve as PRFs “without modification.” What if one has a PRF and wishes to build a PRP from it? This can also be done, but it requires more work. The standard technique was proposed by Luby and Rackoff and it involves building a Feistel network, where each “round function” in the PRP is built using a pseudorandom function. (See the picture at right.) This is a bit more involved than I want to get in this post, so please just take away the notion that the existence of one of these objects implies the existence of the other.

Why do I care about any of this?

I mean, you don’t have to. However: I find that many people just getting into cryptography tend to get very involved in the deep details of particular constructions (ciphers and elliptic curves being one source of rabbit-holing) and take much longer to learn about useful analysis tools like PRFs and PRPs.

Once you understand how PRPs and PRFs work, it’s much easier to think about protocols like block cipher modes of operation, or MAC constructions, or anything that involves deriving multiple keys.

Take a simple example, the CBC mode of operation: this is a “classical” mode of operation used in many block ciphers. I don’t recommend that you use it (there are better modes) but it’s actually a very good teaching example. CBC encryption requires the sender to first select a random string called an Initialization Vector, then to chop up their message into equal-size blocks. Encryption looks something like this:

If we’re willing to assume that the block cipher is a PRP, then analyzing the security of this construction shouldn’t be terribly hard. Provided the block size of the cipher is large enough, we can first use the PRP/PRF switching lemma to argue that a PRP is (computationally) indistinguishable from a random function. To think about the security of CBC-mode encryption, therefore, we can (mathematically) replace our block cipher with a random function of the appropriate domain and range. Now the question is whether CBC-mode is secure when realized with a random function.

So if we replace the block cipher with a random function, how does the argument work?

Well obviously in a real scheme both the encryptor and decryptor would need to have a copy of the same function, and we’ve already covered why that’s problematic: the function would need to be fully-sampled and then communicated between the two parties. Then they would have to scan through a massive table to find each entry. But let’s put that aside for a moment.

Instead let’s focus only on the encryptor. Since we don’t have to think about communicating the entire function to another party, we don’t have to sample it up front. Instead we can sample it “lazily” for the purposes of arguing security.

More specifically: means instead of sampling the entire random function in one go, we can instead imagine using an oracle that “builds” the function one query at a time. The oracle works as follows: anytime the encryptor queries it on some input value, the oracle checks to see if this value has been queried before. If it has previously been queried, the oracle outputs the value it gave previously. Otherwise it samples a new (uniformly random) output string using a random number generator, then writes the input/output values down so it can check for later duplicate inputs.

Now imagine that an encryptor is using CBC mode to encrypt some secret message, but instead of a block cipher they are using our “random function” oracle above. The encryption of a message will work like this:

To encrypt each new message, the encryptor will first choose a uniformly-random Initialization Vector (IV).
She will then XOR that IV with the first block of the message, producing a uniformly-distributed string.
Then she’ll query the random function oracle to obtain the “encipherment” of this string. Provided the oracle hasn’t seen this input before, it will sample and output a uniformly random output string. That string will form the first block of ciphertext.
Then the encryptor will take the resulting ciphertext block and treat it as the “IV” for the next message block, and will repeat steps (2-4) over and over again for each subsequent block.

Notice that this encryption is pretty good. As long as the oracle never gets called on the same input value twice, the output of this encryption process will be a series of uniformly-random bits that have literally nothing to do with the input message. This strongly imples that CBC ciphertexts will be very secure! Of course we haven’t really proven this: we have to consider the probability that the encryptor will query the oracle twice on the same input value. Fortunately, with a little bit of simple probability, we can show the following: since (1) each input is uniformly distributed, then (2) the probability of such a repeated input stays quite low.

(In practice the probability works out to be a function of the function’s output length and the total number of plaintext blocks enciphered. This analysis is part of the reason that cryptographers generally prefer ciphers with large block sizes, and why we place official limits on the number of blocks you’re allowed to encipher with modes like CBC before you change the key. To see more of the gory details, look at this paper.)

Notice that so far I’ve done this analysis assuming that the block cipher (encipherment) function is a random function. In practice, it makes much more sense to assume that the block cipher is actually a pseudorandom permutation. Fortunately we’ve got most of the tools to handle this switch. We need to add two final details to the intuition: (1) since a PRF is indistinguishable from a random function to all bounded adversaries, we can first substitute in a PRF for that random function oracle with only minimal improvement in the attacker’s ability to distinguish the ciphertext from random bits. Next: (2) by the PRP/PRF switching lemma we can exchange that PRF for a PRP with similarly minor impact on the adversary’s capability.

This is obviously not a proof of security: it’s merely an intuition. But it helps to set up the actual arguments that would appear in a real proof. And you can provide a similar intuition for many other protocols that use keyed PRF/PRP type functions.

What if the PRP/PRF key isn’t secret?

One of the biggest restrictions on the PRF concept is the notion that these functions are only secure when the secret key (AKA, the choice of which “function” to use from the family) is kept secret from the adversary. We already discussed why this is critical: in the PRF (resp. PRP) security game, an attacker who learns the key can instantly “distinguish” a pseudorandom function from a random one. In other words, knowledge of the secret key explodes the entire concept of pseudorandomness. Hence from a mathematical perspective, the security properties of a PRF are somewhere between non-existent and undefined in this setting.

But that’s not very satisfying, and this kind of non-intuitive behavior only makes people ask more questions. They come back wondering: what actually happens when you learn the secret key for a PRF? Does it explode or collapse into some kind of mathematical singularity? How does a function go from “indistinguishable from random” to “completely broken” based on learning a small amount of data?

And then, inevitably, they’ll try to build things like hash functions using PRFs.

The former questions are mainly interesting to cryptographic philosophers. However the latter question is practically relevant, since people are constantly trying to do things like build hash functions out of block ciphers. (NB: this is not actually a crazy idea. It’s simply not possible to do it based solely on the assumption that these functions are pseudorandom.)

So what happens to a PRF when you learn its key?

One answer to this question draws from the following (tempting, but incorrect) line of reasoning: PRFs must somehow produce statistically-“random looking” output all the time, whether you know the key or not. Therefore, the argument goes, the PRF is effectively as good as random even after one learns the key.

This intuition is backed up by the following thought-experiment:

Imagine that at time (A) I do not know the key for a PRF, but I query an oracle on a series of inputs (for simplicity, let’s say I use the values 1, 2, …, q for some integer q that is polynomial in the key length.)
Clearly at this point, the outputs of the PRF must be indistinguishable from those of a true random function. If the range of the function comprises $\ell$ -bit strings, then any statistical “randomness test” I run on those outputs should “succeed”, i.e., tell me that they look pretty random.
(Putting this differently: if any test reliably “fails” on the output of the PRF oracle, but “succeeds” on the output of a true random function, then you’ve just built a test that lets you distinguish the PRF from a random function — and this means the function was never a PRF in the first place! And your “PRF” will now disappear in a puff of logic.)
Now imagine that at time (B) — after I’ve obtained the oracle outputs — someone hands me the secret key for the PRF that was inside the oracle. Do the outputs somehow “stop” being random? Will the NIST test suite suddenly start failing?

The simple answer to the last question is “obviously no.” Any public statistical test you could have performed on the original outputs will still continue to pass, even after you learn the secret key. What has changed in this instance is that you can now devise new non-public statistical tests that are based on your knowledge of the secret key. For example, you might test to see if the values are outputs of the PRF (on input the secret key), which of course they would be — and true random numbers wouldn’t be.

So far this doesn’t seem so awful.

Where things get deeply unpleasant is if the secret key is known to the attacker at the time it queries the oracle. Then the calls to the PRF can behave in ways that deviate massively from the expected behavior of a random function. For example, consider a function called “Katy-Perry-PRF” that generally behaves like a normal PRF most of the time, but that spews out Katy Perry lyrics when queried on specific (rare) inputs.

Provided that these rare inputs are hard for any attacker to find — meaning, the attacker will find them only with negligible probability — then Katy-Perry-PRF will be a perfectly lovely PRF. (More concretely, we might imagine that the total number of possible input values is exponential in the key length, and the set of “Katy-Perry-producing” input values forms a negligible fraction of this set, distributed pseudorandomly within it, to boot.) We can also imagine that the location of these Katy-Perry-producing inputs is only listed in the secret key, which a normal PRF adversary will not have.

Clearly a standard attacker (without the secret key) is unlikely to find any inputs that produce Katy Perry lyrics. Yet an attacker who knows the secret key can easily obtain the entire output of Katy Perry’s catalog: this attacker will simply look through the secret key to find the appropriate inputs, and then query them all one at a time. The behavior of the Katy-Perry function on these inputs is clearly very different from what we’d expect from a random function and yet here is a function that still satisfies the definition of a PRF.

Now obviously Katy-Perry-PRF is a silly and contrived example. Who actually cares if your PRF outputs Katy Perry lyrics? But similar examples can be used to produce PRFs that enable easy “collisions”, which is generally a bad thing when one is trying to build things like hash functions. This is why the construction of such functions needs to either assume weaker properties (i.e., that you get only collision-resistance) or make stronger assumptions, such as the (crazy) assumption that the block cipher is actually a random function.

Finally: how do we build PRFs?

So far I’ve been using the ChaCha function as an example of something we’d really like to imagine is a PRF. But the fact of the matter is that nobody knows how to actually prove this. Most of the practical functions we use like PRFs, which include ChaCha, HMAC-SHA(x), and many other ciphers, are constructed from a handful of simple mathematical operations such as rotations, XORs, and additions. The result is then analyzed by very smart people to see if they can break it. If someone finds a flaw in the function, we stop using it.

This is theoretically less-than-elegant. Instead, it would be nice to have constructions we clearly know are PRFs. Unfortunately the world is not quite that friendly to cryptography.

From a theoretical perspective, we know that PRFs can be constructed from pseudorandom generators (PRGs). We further know that PRGs can in turn be constructed from one-way functions (OWFs). The existence of the latter functions is one of the most basic assumptions we make in cryptography, which is a good way of saying we have no idea if they exist but we are hopeful. Indeed, this is the foundation of what’s called the “standard model.” But in practice the existence of OWFs remains a stubbornly open problem, bound tightly to the P/NP problem.

If that isn’t entirely satisfying to you, you might also like to know that we can also build (relatively) efficient PRFs based on the assumed hardness of a number of stronger mathematical assumptions, including things like the Decisional Diffie-Hellman assumption and various assumptions in lattices. Such things are nice mainly because they let us build cool things like oblivious PRFs.

Phew!

This has been a long piece, on that I’m glad to have gotten off my plate. I hope it will be helpful to a few people who are just starting out in cryptography and are itching to learn more. If you are one of these people and you plan to keep going, I urge you to take a look at a cryptography textbook like Katz/Lindell’s excellent textbook, or Goldreich’s (more theoretical) Foundations of Cryptography.

Top photo by Flickr user Dave DeSandro, used under CC license.