"In theory, theory and practice are the same. In practice they are not" -Quote from somebody on the internet. Also attributed to Albert Einstein but I've never been able to find the original source to back that up.

Back-story:

Currently I'm writing a post looking into Hashcat's Markov mode but I found myself starting off by including several paragraphs worth of disclosures and caveats. Or to put it another way:

It was a valid point Jeremi brought up and it's something I'm trying to avoid. After thinking about it for a bit I figured this topic was worth its own post.

Precision vs Recall: 

Part of the challenge I'm dealing with is I'm performing experiments vs writing tutorials. That's not to say I won't write tutorials in the future but designing and running tests to evaluate algorithms is fun and what I'm interested in right now. Why this can be a problem though is that I can get so deep into how an algorithm works that it's easy to loose sight of how it performs in a real life cracking session. I try to be aware of this, but an additional challenge is representing these investigations to everyone else in a way that isn't misleading.

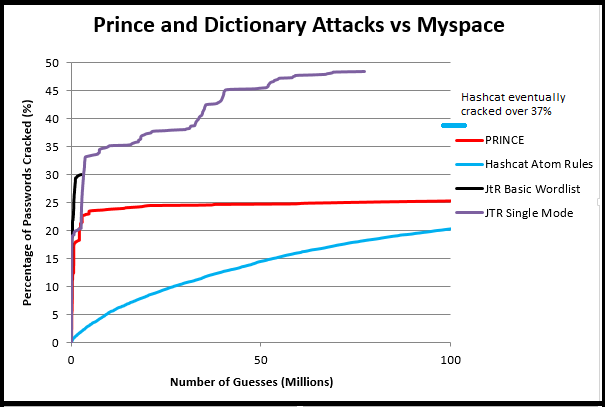
This gets into the larger issue of balancing precision and recall. In a password cracking context, precision is modeling how effective each guess is when it comes to cracking a password. The higher your precision, the fewer guesses on average you need to make to crack a password. As a rule of thumb if you see a graph with number of guesses on the X axis and percentage of passwords cracked on the Y axis, it's probably measuring precision.

An example of measuring the precision of different cracking techniques

Recall on the other hand is the percentage of passwords cracked during a cracking session in total, regardless of how many guesses are made. Usually this isn't represented in a graph format, and if it is, the X axis will be represented by "Time", and not number of guesses.

Courtesy of Korelogic's Crack Me If You Can contest. This represents a Recall based graph

It's tempting to say that "Precision" is a theoretical measurement and "Recall" is the practical results. It's not quite so clear cut though since the "time" factor in password cracking generally boils down to "number of guesses". In an online guessing scenario an attacker may only be able to make 10-20 guesses. With a fast hash, offline attack, and a moderate GPU setup, billions of guesses a second are possible and an attack might run for several weeks. Therefore recall results tend to be highly dependent of the particular situation being modeled.

Now it would be much easier to switch between "Precision" and "Recall" if there was a direct mapping between number of guesses and time. The problem is, not all guesses take the same amount of time. A good example of that is CPU vs GPU based guessing algorithms. Going back to John the Ripper's Incremental mode, I'm not aware of any GPU implementation of it so guesses have to be generated by the CPU and then sent to the GPU for hashing. Meanwhile Hashcat's Markov mode can run in the GPU itself, and in Atom's words "it has to create 16 billions candidates per 10 milliseconds on a single GPU. Yes, billions". Therefore this can lead to situations such in the case of a very fast hash where certain attacks might have a higher precision, but worse recall.

Amdahl's law and why I find precision interesting

When trying to increase recall an attacker generally has two different avenues to follow. They can increase the number of guesses they make or they can increase the precision of the guesses they make. These improvements aren't always exclusive; many times you can do both. Often though there is a balancing act as more advanced logic can take time and may be CPU bound. What this means is that you might increase precision only to find your recall has fallen since you are now making fewer guesses. That being said, if the increase in precision is high enough, then even an expensive guessing algorithm might do well enough to overcome the decrease in the total number of guesses it can make.

Often in these optimization situations Amdahl's law pops into my head, though Gustafson's law might be more appropriate for password cracking due to the rate of increase in the number of guesses. Amdahl's law in a nutshell says the maximum speedup you can have is always limited by the part of the program you can't optimize. To put it another way, if you reduce the cost of an action by 99%, but that action only accounts for 1% of the total run-time, then your maximum total speedup no matter how cool your optimization is would be no more than 1%.

Where this applies to password cracking is the cost of  a guess in an offline cracking attack can be roughly modeled as:

Cost of making the plain-text guess + cost of hashing + general overhead of the cracking tool

Right now the situation in many cases is that the cost of hashing is low thanks to fast unsalted hashing algorithms and GPU based crackers. Therefore it makes sense to focus on reducing the cost of making the plain-text guesses as much as possible since that will have a huge impact on the overall cost of making a guess. Aka, trading precision for speed in your guessing algorithm can have a significant impact on the total number of guesses you can make. If on the other hand a strong hash is used, (or you at least are trying to crack a large number of uniquely salted hashes), the dominant factor in the above equation becomes the hashing itself. Therefore a speedup in the plaintext generation will not have as much impact on the overall cost and therefore precision becomes more important.

As a researcher, precision is very interesting for me. From a defensive standpoint a good starting place is "use a computationally expensive salted hash". If you aren't at least doing that then the chances are you aren't interested in doing anything more exotic. Also when it comes to contributing to the larger research community, well my coding skills are such that I'm not going to be making many improvements to the actual password cracking tools. Evaluating and improving the precision of different attacks is much more doable.

Carnegie Mellon's Password Guessability Service:

The service itself is free to ethical security researchers and is run by students so don't be a jerk. The actual attacks they run are bound to change with time, but as of right now they are offering to model several different default password cracking attacks consisting of around 10 trillion guesses each. These cracking attacks use the public TrustWave's JtR KoreLogic Rulelist, several different HashCat rulesets, an updated Probabilistic Context Free Grammar attack, and another custom attack designed by Korelogic specifically for this service. All in all, if you need to represent an "industry standard" cracking session it's hard to do better. In fact it probably represents a much more advanced attacker than many of the adversaries out there if you assume the target passwords were protected by a hashing algorithm of moderate strength.

I could keep on talking about this service but you really should just read their paper first. I think it's a wonderful resource for the research community and I have lots of respect for them offering this. So the next question of course is what does that mean for this blog? I plan on using this service as it makes sense without hogging Carnegie Mellon's resources. I need to talk to them more about it but I expect that I'll  have them run it against a subset of the RockYou list and then use, and reuse, those results to evaluate other cracking techniques as I investigate them. If I attack some other dataset though I may just run a subset of the attacks myself, unless that dataset and the related tests are interesting enough to make using CM's resources worth it.

Fun with Designing Experiments:

When designing experiments there's usually a couple of common threads I'm always struggling with:

1. Poor datasets. I know there's a ton of password dumps floating around but often due to the nature of their disclosure there's massive problems or shortcomings with most of them. For example most of the dumps on password cracking forums or pastebin have only unique hashes, so '123456' only shows up once, and there is no attribution. Gawker was a site most people didn't care about and the hashing algorithm cut off the plaintext after 8 characters and replaced non-ASCII text as a '?'. A majority of the passwords in the Stratfor dataset were machine generated. Myspace, well that was a result of a phishing attack so it has many instances of 'F*** You You F***ing Hacker'. Even with RockYou the dataset is complicated as it contained many passwords from the same users for different sites but since there were no usernames connected with the public version of it, it can be hard to sort out. Then there is the fact that most of these datasets were for fairly unimportant sites. I'm not aware of any confirmed public Active Directory dump, (though there are a large number of NT hashes floating about and this whole Ashley Madison hack may change things with the Avid Life Media NT hashes there). Likewise, while there are some banking password lists, the amount of drama surrounding them makes me hesitant to use them.
2. Short running time. Personally I like keeping the time it takes to run a test to around an hour or so. While I can certainly run longer tests, realistically anything over a couple of days isn't going to happen since I like using my computers for other things and truth be told, it always seems like I end up finding out I need to run additional tests or I messed something up in my original setup and need to re-run it. Shorter tests are very much preferred. Add into that the fact that most of the time I'm modeling precision and running my tests on a CPU system means most of my tests will not be modeling GPU cracking vs fast hashes.
3. What hypothesis do I want to test, and can I design an experiment to test it? I'll admit, sometimes I'll have no clue what the results of a test will be so I'll pull a YOLO, throw some stuff together and just run it to see what pops out. That's not ideal though as I usually like to try and predict the results. I'm often wrong, but that at least forces me to look deeper into what assumptions I held were wrong, and hey that's why I run tests in the first place.

Furthermore, for at least the next couple of tools I'm investigating I plan on using both Hashcat and John the Ripper as much as possible. While it might not always make sense to use both of them as often there isn't an apples to apples comparison, I do have some ulterior motives. Basically it helps me to use both of these tools in a public setting and I've already gotten a lot of positive feedback from my PRINCE post. It's pretty amazing when I can have a creator of a tool tell me how I can optimize my cracking techniques. My secondary reason for this is to make people more aware of both of these tools. When it comes to the different attack modes I've found there's a lot of misunderstandings of what each tool is capable of.

Thanks for putting up with all of that text. In the spirit of showing all my research I'm sharing the tool that I wrote to evaluate password cracking sessions which I'll be using in this blog. The code is available here:

The specific tool I'm talking about, (in the hope that I release multiple tools in the future so it isn't obvious ;p), is called checkpass2.py. It's a significantly faster version of the old checkpass program I had used and released in the past. The options on how it works are detailed in the -h switch, but basically you can pipe whatever password guess generation tool you are using into it and it'll compare your guesses against a plaintext target list and tell you how effective your cracking session would have been. For example if you were using John the Ripper you could use the -stdout option to model a cracking session as follows:

./john -wordlist=passwords.lst -rules=single -stdout | python checkpass2.py -t target.pws -o results.txt

It also has some options like limiting the maximum number of guesses or starting a count at a specific number if you want to chain multiple cracking sessions together. There's certainly still a lot of improvements that need to be made to it, but if you like graphs I hope it might be useful to you. Please keep in mind that this isn't a password cracker. Aka, It does not do any hashing of password guesses. So if you want to model a password cracking session against a hashed list you'll need to run two attacks, One to crack the list using the tool of your choice, and a second session to use the checkpass2.py tool to model your cracking session against the cracked passwords. Since both John the Ripper and Hashcat have logging options you might want to consider using them instead to save time. Where checkpass2 is nice for me anyway is the fact that I can quickly edit the code depending on what I need so it's easier to do things like format the output for what I'm doing. Long story short, I hope it is helpful but I still strongly recommend looking into the logging options that both John the Ripper and Hashcat offer.