There are many obfuscators for different languages, and some of those offer reversible options for easier field debugging. Eazfuscator.NET is one of these and with a bit of reverse engineering, whole files can be restored with the original symbols once you have the password.

In our case, the developer left the password in some of the files, as the encryption reads the password from a directive that gets compiled into the executable binary. The obfuscator then reads this later in the pipeline, however, the developers missed this step in case of some executables, thus we had the password.

However, even with the password, the only thing you could do was use their official decryptor, which

• uses a GUI, thus limits automation and
• limits the length to that of a typical stack trace.

Hence our journey began to find the exact cryptographic construct they used. The documentation linked above reveals that

Used crypto algorithm is AES with 256 bits key strength. Cryptographic key for the algorithm is derived from the password.

This left us with an unknown box that takes a password and spits out a 256-bit key for the AES process. We also didn’t know what block chaining method was used, so all this had to be reverse engineered from the official decryptor. Latter was also a .NET application, so we used dnSpy, a very handy tool licensed under GPLv3 for both static and dynamic analysis of such executables.

A nice twist was that this official decryptor, as part of an obfuscator suite was also using the obfuscator on itself, stripping symbols of human-readable names and making comparison between symbols harder.

Educated guessing is always an important part of reverse engineering, and this case was no exception: most people use PBKDF2 to derive cryptographic keys from human readable strings such as passwords, as it’s well-known and cryptographic libraries for most platforms include it. In .NET’s built-in System.Security.Cryptography the class implementing this is called Rfc2898DeriveBytes as PBKDF2 is defined in section 5.2 of RFC 2898.

As dnSpy struggled with the optimizations in the binaries caused by them being release builds, we had to be careful to stop execution in those places where we had access to memory. We’ve started to hate the common error message:

Can’t evaluate when the thread is at an unsafe point. Step once or run until a breakpoint hits.

But finally, we managed to find a good spot in the GetBytes method which returns the actual PBKDF2 output.

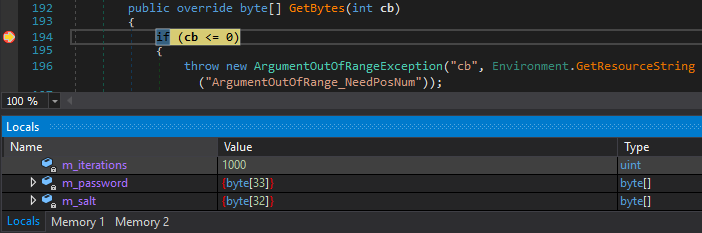
As it can be seen above, the number of iterations was 1000, which is the default in the .NET implementation. From this, we also guessed that the hash function used as the parameter of PBKDF2 was also the default, HMAC-SHA-1, which also proved to be right.

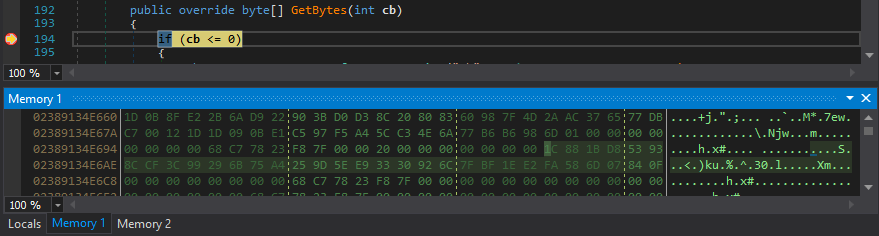
Looking at the memory also revealed the salt, the above one was used to generate the IV, and another static salt was used to derive the actual AES key. It seemed so that they used AES in CBC mode, deriving the IV from the password in the same way as with the key, only they used a different salt.

With this in place, we still had two obstacles in the way. For some reason, they decided to use a subset of printable characters, thus they encoded it in a way that looked like Base64. The character set matched for the most part: the usual alphanumerics resulted in 62 symbols, and for the remaining two they chose '$' and '_'. What puzzled us was that although most libraries agree in that the so-called URL-safe Base64 encoding uses '-' and '_' as the two non-alphanumeric symbols, Eazfuscator.NET’s encoding used '_' at the other position, resulting in quite a few minutes worth of confusion as to why the simple urlsafe_b64decode(input.replace('$', '-')) didn’t work but rather produced gibberish when decrypted.

Fortunately, they used PKCS7 padding, so the success of the decryption could be determined as soon as the above decoding problem was settled. If you know how PKCS7 padding works and already understand how it helped us at this stage, just skip to the next paragraph – if not, here’s a short rundown. When using a block cipher like AES to encrypt messages whose length is not an exact multiple of the block size (128 bits = 16 bytes for AES), one needs to append padding bytes to pad the message. PKCS7 is a widely used algorithm that calculates how many bytes you need to append to fill the last block and every pad byte has the value of this number. So if the block size is 16 bytes and the last block would have only 14 bytes, it’ll append the following 2 bytes: 0x02 0x02. If the message is lucky to fill the last block by itself already, a full block of padding is added. This way, checking whether the decryption was successful is easy, as one just has to look at the last byte (let’s call it n) and check whether the n-1 are also the same value. (This is also how padding oracles work.)

This was important since the other obstacle was a rather annoying one. Using the official decryptor, we already had some plaintext-ciphertext pairs and now we saw an interesting pattern. When decrypting a ciphertext where we knew the plaintext to be 20 bytes, our own reimplementation of the decryption process resulted in 21 seemingly garbage bytes.

Further dynamic analysis proved that they had a last layer of defense in the form of XORing the plaintext before AES encryption with a single byte, and appending this byte to the plaintext. Removing this trailing byte and performing the XOR operation on all the remaining bytes resulted in the expected symbol name.

Our Python reimplementation is available in our GitHub repository under MIT license, pull requests are welcome.