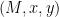Warning: extremely wonky cryptography post. Also, possibly stupid and bound for nowhere.

One of the hardest problems in applied cryptography (and perhaps all of computer science!) is explaining why our tools work the way they do. After all, we’ve been gifted an amazing basket of useful algorithms from those who came before us. Hence it’s perfectly understandable for practitioners to want to take those gifts and simply start to apply them. But sometimes this approach leaves us wondering why we’re doing certain things: in these cases it’s helpful to take a step back and think about what’s actually going on, and perhaps what was in the inventors’ heads when the tools were first invented.

In this post I’m going to talk about signature schemes, and specifically the Schnorr signature, as well as some related schemes like ECDSA. These signature schemes have a handful of unique properties that make them quite special among cryptographic constructions. Moreover, understanding the motivation of Schnorr signatures can help understand a number of more recent proposals, including post-quantum schemes like Dilithium — which we’ll discuss in the second part of this series.

As a motivation for this post, I want to talk about this tweet:

Instead of just dumping Schnorr signatures onto you, I’m going to take a more circuitous approach. Here we’ll start from the very most basic building blocks (including the basic concept of an identification protocol) and then work our way gradually towards an abstract framework.

Identification protocols: our most useful building block

If you want to understand Schnorr signatures, the very first thing you need to understand is that they weren’t really designed to be signatures at all, at least not at first. The Schnorr protocol was designed as an interactive identification scheme, which can be “flattened” into the signature scheme we know and love.

An identification scheme consists of a key generation algorithm for generating a “keypair” comprising a public and secret key, as well as an interactive protocol (the “identification protocol”) that uses these keys. The public key represents its owners’ identity, and can be given out to anyone. The secret key is, naturally, secret. We will assume that it is carefully stored by its owner, who can later use it to prove that she “owns” the public key.

The identification protocol itself is run interactively between two parties — meaning that the parties will exchange multiple messages in each direction. We’ll often call these parties the “prover” and the “verifier”, and many older papers used to give them cute names like “Peggy” and “Victor”. I find this slightly twee, but will adopt those names for this discussion just because I don’t have any better ideas.

To begin the identification protocol, Victor must obtain a copy of Peggy’s public key. Peggy for her part will possess her secret key. The goal of the protocol is for Victor to decide whether he trusts Peggy:

Note that this “proof of ownership” does not need to be 100% perfect. We only ask that it is sound with extremely high probability. Roughly speaking, we want to ensure that if Peggy really owns the key, then Victor will always be convinced of this fact. At the same time, someone who is impersonating Peggy — i.e., does not know her secret key — should fail to convince Victor, except with some astronomically small (negligible) probability.

(Why do we accept this tiny probability of an impersonator succeeding? It turns out that this is basically unavoidable for any identification protocol. This is because the number of bits Peggy sends to Victor must be finite, and we already said there must exist at least one “successful” response that will make Victor accept. Hence there clearly exists an adversary who just guesses the right strings and gets lucky very ocasionally. As long as the number of bits Peggy sends is reasonably large, then such a “dumb” adversary should almost never succeed, but they will do so with non-zero probability.)

The above description is nearly sufficient to explain the security goals of an identification scheme, and yet it’s not quite complete. If it was, then there would be a very simple (and yet obviously bad) protocol that solves the problem: the Prover could simply transmit its secret key to the Verifier, who can presumably test that it matches with the public key:

If all we cared about was solving the basic problem of proving ownership in a world with exactly one Verifier who only needs to run the protocol once, the protocol above would work fine! Unfortunately in the real world we often need to prove identity to multiple different Verifiers, or to repeatedly convince the same Verifier of our identity. The problem with the strawman proposal above is that at the end of a single execution, Victor has learned Peggy’s secret key (as does anyone else who happened to eavesdrop on their communication.) This means that Victor, or any eavesdropper, will now be able to impersonate Peggy in future interactions.

And that’s a fairly bad feature for an identification protocol. To deal with this problem, a truly useful identification protocol should add at least one additional security requirement: at the completion of this protocol, Victor (or an eavesdropper) should not gain the ability to mimic Peggy’s identity to another Verifier. The above protocol clearly fails this requirement, since Victor will now possess all of the secret information that Peggy once had.

This requirement also helps to why identification protocols are (necessarily) interactive, or at least stateful: even if Victor did not receive Peggy’s secret key, he might still be able to record any messages sent by Peggy during her execution of the protocol with him. If the protocol was fully non-interactive (meaning, it consists of exactly one message from Peggy to Victor) then Victor could later “replay” his recorded message to some other Verifier, thus convincing that person that he is actually Peggy. Many protocols have suffered from this problem, including older vehicle immobilizers.

The classical solution to this problem is to organize the identification protocol to have a challenge-response structure, consisting of multiple interactive moves. In this approach, Victor first sends some random “challenge” message to Peggy, and then Peggy then constructs her response so that it is specifically based on Victor’s challenge. Should a malicious Victor attempt to impersonate Peggy to a different Verifier, say Veronica, the expectation is that Veronica will send a different challenge value (with high probability), and so Victor will not be able to use Peggy’s original response to satisfy Veronica’s new challenge.

(While interaction is generally required, in some instances we can seemingly “sneak around” this requirement by “extracting a challenge from the environment.” For example, real-world protocols will sometimes ‘bind’ the identification protocol to metadata such as a timestamp, transaction details, or the Verifier’s name. This doesn’t strictly prevent replay attacks — replays of one-message protocols are always possible! — but it can help Verifiers detect and reject such replays. For example, Veronica might not accept messages with out-of-date timestamps. I would further argue that, if one squints hard enough, these protocols are still interactive. It’s just that the first move of the interaction [say, querying the clock for a timestamp] is now being moved outside of the protocol.)

How do we build identification schemes?

Once you’ve come up with the idea of an identification scheme, the obvious question is how to build one.

The simplest idea you might come up with is to use some one-way function as your basic building block. The critical feature of these functions is that they are “easy” to compute in one direction (e.g., for some string x, the function F(x) can be computed very efficiently.) At the same time, one-way functions are hard to invert: this means that given F(x) for some random input string x — let’s imagine x is something like a 128-bit string in this example — it should take an unreasonable amount of computational effort to recover x.

I’m selecting one-way functions because we have a number of candidates for them, including cryptographic hash functions as well as fancier number-theoretic constructions. Theoretical cryptographers also prefer them to other assumptions, in the sense that the existence of such functions is considered to be one of the most “plausible” cryptographic assumptions we have, which means that they’re much likelier to exist than more fancy building blocks.

The problem is that building a good identification protocol from simple one-way functions is challenging. An obvious starting point for such a protocol would be for Peggy to construct her secret key by selecting a random string sk (for example, a 128-bit random string) and then computing her public key as pk = F(sk).

Now to conduct the identification protocol, Peggy would… um… well, it’s not really clear what she would do.

The “obvious” answer would be for Peggy to send her secret key sk over to Victor, and then Victor could just check that pk = F(sk). But this is obviously bad for the reasons discussed above: Victor would then be able to impersonate Peggy after she conducted the protocol with him even one time. And fixing this problem turns out to be somewhat non-trivial!

There are, of course, some clever solutions — but each one entails some limitations and costs. A “folklore”¹ approach works like this:

1. Instead of picking one secret string, Peggy picks N different secret strings to be her “secret key.”
2. She now sets her “public key” to be .
3. In the identification protocol, Victor will challenge Peggy by asking her for a random k-sized subset of Peggy’s strings (here k is much smaller than N.)
4. Peggy will send back the appropriate list of k secret strings.
5. Victor will check each string against the appropriate position in Peggy’s public key.

The idea here is that, after running this protocol one time, Victor learns some but not all of Peggy’s secret strings. If Victor was then to attempt to impersonate Peggy to another person — say, Veronica — then Veronica would pick her own random subset of k strings for Victor to respond to. If this subset is identical to the one Victor chose when he interacted with Peggy, then Victor will succeed: otherwise, Victor will not be able to answer Veronica’s challenge. By carefully selecting the values of N and k, we can ensure that this probability is very small._²

An obvious problem with this proposal is that it falls apart very quickly if Victor can convince Peggy to run the protocol with him multiple times.

If Victor can send Peggy several different challenges, he will learn many more than k of Peggy’s secret strings. As the number of strings Victor learns increases, Victor’s ability to answer Veronica’s queries will improve dramatically: eventually he will be able to impersonate Peggy nearly all of the time. There are some clever ways to address this problem while still using simple one-way functions, but they all tend to be relatively “advanced” and costly in terms of bandwidth and computation. (I promise to talk about them in some other post.)

Schnorr

So far we have a motivation: we would like to build an identification protocol that is multi-use — in the sense that Peggy can run the protocol many times with Victor (or other verifiers) without losing security. And yet one that is also efficient in the sense that Peggy doesn’t have to exchange a huge amount of data with Victor, or have huge public keys.

Now there have been a large number of identity protocols. Schnorr is not even the first one to propose several of the ideas it uses. “Schnorr” just happens to be the name we generally use for a class of efficient protocols that meet this specific set of requirements.

Some time back when Twitter was still Twitter, I asked if anyone could describe the rationale for the Schnorr protocol in two tweets or less. I admit I was fishing for a particular answer, and I got it from Chris Peikert:

I really like Chris’s explanation of the Schnorr protocol, and it’s something I’ve wanted to unpack for while now. I promise that all you really need to understand this is a little bit of middle-school algebra and a “magic box”, which we’ll do away with later on.

Let’s tackle it one step at a time.

First, Chris proposes that Peggy must choose “a random line.” Recalling our grade-school algebra, the equation for a line is y = mx + b, where “m” is the line’s slope and “b” its y-intercept. Hence, Chris is really asking us to select a pair of random numbers (m, b). (For the purposes of this informal discussion you can just pretend these are real numbers in some range. However later on we’ll have them be elements of a very large finite field or ring, which will eliminate many obvious objections.)

Here we will let “m” be Peggy’s secret key, which she will choose one time and keep the same forever. Peggy will choose a fresh random value “b” each time she runs the protocol. Critically, Peggy will put both of those numbers into a pair of Chris’s magic box(es) and send them over to Victor.

Finally, Victor will challenge Peggy to evaluate her line at one specific (random) point x that he selects. This is easy for Peggy, who can compute the corresponding value y using her linear equation. Now Victor possesses a point (x, y) that — if Peggy answered correctly — should lie on the line defined by (m, b). He simply needs to use the “magic boxes” to check this fact.

Here’s the whole protocol:

Clearly this is not a real protocol, since it relies fundamentally on magic. With that said, we can still observe some nice features about it.

A first thing we can observe about this protocol is that if the final check is satisfied, then Victor should be reasonably convinced that he’s really talking to Peggy. Intuitively, here’s a (non-formal!) argument for why this is the case. Notice that to complete the protocol, Peggy must answer Victor’s query on any random x that Victor chooses. If Peggy, or someone impersonating Peggy, is able to do this with high probability for any random point x that Victor might choose, then intuitively it’s reasonable that she could (in her own head, at least) compute a similar response for a second random point x’. Critically, given two separate points (x,y), (x’, y’) all on the same line, it’s easy to calculate the secret slope m — ergo, a person who can easily compute points on a line almost certainly knows Peggy’s secret key. (This is not a proof! It’s only an intuition. However the real proof uses a similar principle.²)

The question, then, is what Victor learns after running the protocol with Peggy.

If we ignore the magical aspects of the protocol, the only thing that Victor “learns” by at end of the protocol is a single point (x, y) that happens to lie on the random line chosen by Peggy. Fortunately, this doesn’t reveal very much about Peggy’s line, and in particular, it reveals very little about her secret (slope) key. The reason is that for every possible slope value m that Peggy might have chosen as her key, there exists a value b that produces a line that intersects (x, y). We can illustrate this graphically for a few different examples:

Naturally this falls apart if Victor sees two different points on the same line. Fortunately this never happens, because Peggy chooses a different line (by selecting a new b value) every time she runs the protocol. (It would be a terrible disaster if she forgot to do this!)

The existence of these magic boxes obviously makes security a bit harder to think about, since now Victor can do various tests using the “boxes” to test out different values of m, b to see if he can find a secret line that matches. But fortunately these boxes are “magic”, in the sense that all Victor can really do is test whether his guesses are successful: provided there are many possible values of m, this means actually searching for a matching value will take far too long to be useful.

Now, you might ask: why a line? Why not a plane, or a degree-8 polynomial?

The answer is pretty simple: a line happens to be one of the simplest mathematical structures that suits our needs. We require an equation for which we can “safely” reveal exactly one solution, without fully constraining the terms of its equation. Higher-degree polynomials and planar equations also possess this capability (indeed we can reveal more points in these structures), but each has a larger and more complex equation that would necessitate a fancier “magic box.”

How do we know if the “magic box” is magic enough?

Normally when people learn Schnorr, they are not taught about magic boxes. In fact, they’re typically presented with a bunch of boring details about cyclic groups.

The problem with that approach is that it doesn’t teach us anything about what we need from that magic box. And that’s a shame, because there is not one specific box we can use to realize this class of protocols. Indeed, it’s better to think of this protocol as a set of general ideas that can be filled in, or “instantiated” with different ingredients.

Hence: I’m going to try a different approach. Rather than just provide you with something that works to realize our magic box as a fait accompli, let’s instead try to figure out what properties our magical box must have, in order for it to provide us with a secure protocol.

Simulating Peggy

There are essentially three requirements for a secure identification protocol. First, the protocol needs to be correct — meaning that Victor is always convinced following a legitimate interaction with Peggy. Second, it needs to be sound, meaning that only Peggy (and not an impersonator) can convince Victor to accept.

We’ve made an informal argument for both of these properties above. It’s important to note that each of these arguments relies primarily on the fact that our magic box works as advertised — i.e., Victor can reliably “test” Peggy’s response against the boxed information. Soundness also requires that bad players cannot “unbox” Peggy’s secret key and fully recover her secret slope m, which is something that should be true of any one-way function.

But these arguments don’t dwell thoroughly on how secure the boxes must be. Is it ok if an attacker can learn a few bits of m and b? Or do they need to be completely ideal. To address these questions, we need to consider a third requirement.

That requirement is that that Victor, having run the protocol with Peggy, should not learn anything more useful than he already knew from having Peggy’s public key. This argument really requires us to argue that these boxes are quite strong — i.e., they’re not going to leak any useful information about the valuable secrets beyond what Victor can get from black-box testing.

Recall that our basic concern here is that Victor will run the protocol with Peggy, possibly multiple times. At the end of each run of the protocol, Victor will learn a “transcript”. This contents of this transcript are 1) one magic box containing “b“, 2) the challenge value x that Victor chose, and 3) the response y that Peggy answered with. We are also going to assume that Victor chose the value x “honestly” at random, so really there are only two interesting values that he obtained from Peggy.

A question we might ask is: how useful is the information in this transcript to Victor, assuming he wants to do something creepy like pretend to be Peggy?

Ideally, the answer should be “not very useful at all.”

The clever way to argue this point is to show that Victor can perfectly “simulate” these transcripts without every even talking to Peggy at all. The argument thus proceeds as follows: if Victor (all by his lonesome) can manufacture a transcript that is statistically identical to the ones he’d get from talking to Peggy, then what precisely has he “learned” from getting real ones from Peggy at all? Implicitly the answer is: not very much.

So let’s take a moment to think about how Victor might (all by himself) produce a “fake” transcript without talking to Peggy. As a reminder, here’s the “magic box” protocol from up above:

One obvious (wrong) idea for simulating a transcript is that Victor could first select some random value b, and put it into a brand new “magic box”. Then he can pick x at random, as in the real protocol. But this straightforward attempt crashes pretty quickly: Victor will have a hard time computing y = mx + b, since he doesn’t know Peggy’s secret key m. His best attempt, as we discussed, would be to guess different values and test them, which will take too long (if the field is large.)

So clearly this approach does not work. But note that Victor doesn’t necessarily need to fake this transcript “in order.” An alternative idea is that Victor can try to make a fake transcript by working through the protocol in a different order. Specifically:

1. Victor can pick a random x, just as in the real protocol.
2. Now he can pick the value y also at random.
   Note that for every “m” there will exist a line that passes through (x, y).
3. But now Victor has a problem: to complete the protocol, he will need to make a new box containing “b”, such that b = y – mx.

There is no obvious way for Victor to calculate b given only the information he has in the clear. To address this third requirement, we must therefore demand a fundamentally new capability from our magic boxes. Concretely, we can imagine that there is some way to “manufacture” new magic boxes from existing ones, such that the new boxes contain a calculated value. This amounts to reversing the linear equation and then performing multiplication and subtraction on “boxed” values, so that we end up with:

What’s that, you say? This new requirement looks totally arbitrary? Well, of course it is. But let’s keep in mind that we started out by demanding magical boxes with special capabilities. Now I’m simply adding one more magical capability. Who’s to say that I can’t do this?

Recall that the resulting transcript must be statistically identical to the ones that Victor would get from Peggy. It’s easy enough to show that the literal values (x, y, b) will all have the same distribution in both versions. The statistical distribution of our “manufactured magical boxes” is a little bit more complicated, because what the heck does it mean to “manufacture a box from another box,” anyway? But we’ll just specify that the manufactured ones must look identical to the ones created in the real protocol.

Of course back in the real world this matters a lot. We’ll need to make sure that our magical box objects have the necessary features, which are (1) the ability to test whether a given (x, y) is on the line, and (2) the ability to manufacture new boxes containing “b” from another box containing “m” and a point (x, y), while ensuring that the manufactured boxes are identical to magical boxes made the ordinary way.

How do we build a magical box?

An obvious idea might be to place the secret values m and b each into a standard one-way function and then send over F(m) and F(b). This clearly achieves the goal of hiding the values of these two values: unfortunately, it doesn’t let us do very much else with them.

Indeed, the biggest problem with simple one-way functions is that there is only one thing you can do with them. That is: you can generate a secret x, you can compute the one-way function F(x), and then you can reveal x for someone else to verify. Once you’ve done this, the secret is “gone.” That makes simple one-way functions fairly limiting.

But what if F is a different type of one-way function that has some additional capabilities?

In the early 1980s many researchers were thinking about such one-way functions. More concretely, researchers such as Tahir Elgamal were looking at a then-new “candidate” one-way function that had been proposed by Whitfield Diffie and Martin Hellman, for use in their eponymous key exchange protocol.

Concretely: let p be some large non-secret prime number that defines a finite field. And let g be the “generator” of some large cyclic subgroup of prime order q contained within that field.³ If these values are chosen appropriately, we can define a function F(x) as follows:

The nice thing about this function is that, provided g and p are selected appropriately, it is (1) easy to compute this function in the normal direction (using square-and-multiply modular exponentiation) and yet is (2) generally believed to be hard to invert. Concretely, as long x is randomly selected from the finite field defined by {0, …, q-1}, then recovering x from F(x) is equivalent to the discrete logarithm problem.

But what’s particularly nifty about this function is that it has nice algebraic properties. Concretely, given F(a) and F(b) computed using the function above, we can easily compute F(a + b mod q). This is because:

Similarly, given F(a) and some known scalar c, we can compute F(a \cdot c):

We can also combine these capabilities. Given F(m) and F(b) and some x, we can compute F(y) where y = mx + b mod q. Almost magically means we can compute linear equations over values that have been “hidden” inside a one-way function, and then we can compare the result to a direct (alleged) calculation of y that someone else has handed us:

Implicitly, this gives us the magic box we need to realize Chris’s protocol from the previous section. The final protocol looks like this:

Appropriate cyclic groups can also be constructed within certain elliptic curves, such as the NIST P-256 and secp256k1 curve (used for Schnorr signatures in Bitcoin) as well as the EdDSA standard, which is simply a Schnorr signature implemented in the Ed25519 Edwards curve. Here the exponentiation is replaced with scalar point multiplication, but the core principles are exactly the same.

For most people, you’re probably done at this point. You may have accepted my claim that these “discrete logarithm”-based one-way functions are sufficient to hide the values (m, b) and hence they’re magic-box-like.

But you shouldn’t! This is actually a terrible thing for you to accept. After all, modular-exponentiation functions are not magical boxes. They’re real “things” that might potentially leak information about the points “m” and “b”, particularly since Victor will be given many different values to work with after several runs of the protocol.

To convince ourselves that the boxes don’t leak, we must use the intuition I discussed further above. Specifically, we need to show that it’s possible to “simulate” transcripts without ever talking to Peggy herself, given only her public key . Recall that in the discussion above, the approach we used was to pick a random point (x, y) first, and then “manufacture” a box as follows:

In our realized setting, this is equivalent to computing directly from and (x, y). Which we can do as follows:

(If you’re picky about things, here we’re abusing division as shorthand to imply multiplication by the multiplicative inverse of the final term.)

It’s easy enough to see that the implied value b = y – mx is itself distributed identically to the real protocol as long as (x, y) are chosen randomly. In that case it holds that will be distributed identically as well, since there is a one-to-one mapping between between each b and the value in the exponent. This is an extremely convenient feature of this specific magic box. Hence we can hope that this primitive meets all of our security requirements.

From ID protocols to signatures: Fiat-Shamir

While the post so far has been about identification protocols, you’ll notice that relatively few people use interactive ID protocols these days. In practice, when you hear the name “Schnorr” it’s almost always associated with signature schemes. These Schnorr signatures are quite common these days: they’re used in Bitcoin and form the basis for schemes like EdDSA.

There is, of course, a reason I’ve spent so much time on identification protocols when our goal was to get to signature schemes. That reason is due to a beautiful “trick” called the Fiat-Shamir heuristic that allows us to effortlessly move from three-move identification protocols (often called “sigma protocols”, based on the shape of the capital greek letter) to non-interactive signatures.

Let’s talk briefly about how this works.

The key observation of Fiat and Shamir was that Victor doesn’t really do very much within a three-move ID protocol: indeed, his major task is simply to select a random challenge. Surely if Peggy could choose a random challenge on her own, perhaps somehow based off a “message” of her choice, then she could eliminate the need to interact with Victor at all.

In this new setting, Peggy would compute the entire transcript on her own, and she could simply hand Victor a transcript of the protocol she ran with herself (as well as the message.) Provided the challenge value x could be bound “tightly” to a message, then this would convert an interactive protocol like the Schnorr identification protocol into a signature scheme.

One obvious idea would be to take some message M and compute the challenge as x = H(M).

Of course, as we’ve already seen above, this is a pretty terrible idea. If Peggy is allowed to know the challenge value x, then she can trivially “simulate” a protocol execution transcript using the approach described in the previous section — even if she does not know the secret key. The resulting signature would be worthless.

For Peggy to pick the challenge value x by herself, therefore, she requires a strategy for generating x that (1) can only be executed after she’s “committed” to her first magic box containing b, and (2) does not allow her predict or “steer” the value x that she’ll get at the end of this process.

The critical observation made by Fiat and Shamir was that Peggy could do this if she possessed a sufficiently strong hash function H. Their idea was as follows. First, Peggy will generate her value b. Then she will place it into a “magic box” as in the normal protocol (as in the instantiation above.) Finally, she will feed her boxed value(s) for both m and b as well as an optional “message” M into the hash function as follows:

Finally, she’ll compute the rest of the protocol as expected, and hand Victor the transcript which he can check by re-computing the hash function on the inputs to obtain x and verifying that y is correct (as in the original protocol.)

(A variant of this approach has Peggy give Victor a slightly different transcript: here she sends to Victor, who now computes and tests whether . I will leave the logic of this equation for the reader to work out. Commenter Imuli below points to a great StackExchange post that shows all the different variants of Schnorr people have built by using tricks like this.)

For this entire idea to work properly, it must be hard for Peggy to identify a useful input to the hash function that provides an output that she can use to fake the transcript. In practice, this requires a hash function where the “relation” between input and output is what we call evasive: namely, that it is hard to find two points that have a useful relationship for simulating the protocol.

In practice we often model these hash functions in security proofs as though they’re random functions, which means the output is verifiably unrelated to the input. For long and boring reasons, this model is a bit contrived. We still use it anyway.

What other magic boxes might there be?

As noted above, a critical requirement of the “magic box Schnorr” style of scheme is that the boxes themselves must be instantiated by some kind of one-way function: that is, there must be no efficient algorithm that can recover Peggy’s random secret key from within the box she produces, at least without exhaustively testing, or using some similarly expensive (super-polynomial time) attack.

The cyclic group instantiation given above satisfies this requirement provided that the discrete logarithm problem (DLP) is hard in the specific group used to compute it. Assuming your attacker only has a classical computer, this assumption is conjectured to hold for sufficiently-large groups constructed using finite-field based cryptography and in certain elliptic curves.

But nothing says your adversary has to be a classical computer. And this should worry us, since we happen to know that the discrete logarithm problem is not particularly hard to solve given an appropriate quantum computer. This is due to the existence of efficient quantum algorithms for solving the DLP (and ECDLP) based on Shor’s algorithm. To deal with this, cryptographers have come up with a variety of new signature schemes that use different assumptions.

In my next post I’m going to talk about one of those schemes, namely the Dilithium signature scheme, and show exactly how it relates to Schnorr signatures.

This post is continued in Part 2.

Notes:

1. “Folklore” in cryptography means that nobody knows who came up with the idea. In this case these ideas were proposed in a slightly different context (one-time signatures) by folks like Ralph Merkle.
2. Since there are distinct subsets to pick from, the probability that Veronica will select exactly the same subset as Victor did — allowing him to answer her challenge properly — can be made quite small, provided N and k are chosen carefully. (For example, N=128 and k=30 gives about and so Evil Victor will almost never succeed.)
3. Some of these ideas date back to the Elgamal signature scheme, although that scheme does not have a nice security reduction.
4. In the real proof, we actually rely on a property called “rewinding.” Here we can make the statement that if there exists some algorithm (more specifically, an efficient probabilistic Turing Machine) that, given only Peggy’s public key, can impersonate Peggy with high probability: then it must be possible to “extract” Peggy’s secret value m from this algorithm. Here we rely on the fact that if we are handed such a Turing machine, we can run it (at least) twice while feeding in the same random tape, but specifying two different x challenges. If such an algorithm succeeds with reasonable probability in the general case, then we should be able to obtain two distinct points (x, y), (x’, y’) and then we can just solve for (m, b).
5. I’m specifying a prime-order subgroup here not because it’s strictly necessary, but because it’s very convenient to have our “exponent” values in the finite field defined by {0, …, q-1} for some prime q. To construct such groups, you must select the primes q, p such that p = 2q + 1. This ensures that there will exist a subgroup of order q within the larger group defined by the field Fp.