2024-6-8 17:0:16 Author: hackernoon.com(查看原文) 阅读量:2 收藏
Table of Links
- Abstract and Introduction
- Dancing Links
- The Rust Programming Language
- RAC: Hardware/Software Co-Assurance at Scale
- Rust and RAR
- Dancing Links in Rust
- Related Work
- Conclusion, Acknowledgments, and References
2 Dancing Links
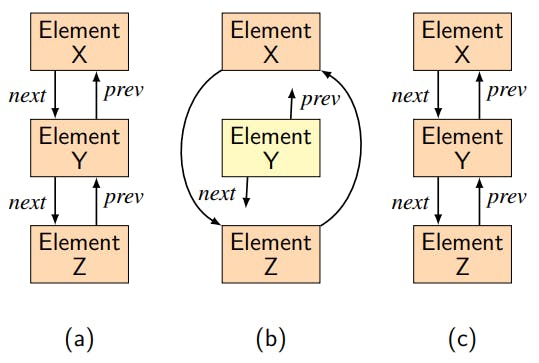
The concept behind Dancing Links is quite simple: when a given element Y of a list is removed in an exact cover algorithm, it is very likely that this same element will later be restored. Thus, rather

than “zero out” the ‘previous’ and ‘next’ links associated with element Y, as good programming hygiene would normally dictate, in Dancing Links, the programmer leaves the link values in place for the removed element. The Dancing Links remove operator thus deletes element Y from the list, setting the ’next’ element of the preceding element X to the following element Z, and setting the ’previous’ element of Z to a link to X, but not touching the ’next’ and ’previous’ links of the removed element Y. Later on, if Y needs to be restored, it is simply hooked back in to the list using a simple restore operator. In Knuth’s words, if one monitors the list links as the DLX algorithm proceeds, the links appear to ‘dance’, hence the name. Knuth’s Dancing Links functionality is summarized in Fig. 1.
如有侵权请联系:admin#unsafe.sh