Blowing Out the Candles on the Birthday Bound

Blowing Out the Candles on the Birthday Bound
2024-7-2 01:17:23 Author: soatok.blog(查看原文) 阅读量:11 收藏

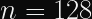
Four years ago, I wrote a (surprisingly popular) blog post about the notion of wear-out for symmetric encryption schemes.

Two years ago, I wrote a thing about extending the nonce used by AES-GCM without introducing foot-guns. This was very recently referenced in one of Filippo Valsorda’s Cryptography Dispatches, which referenced alternative designs in the same vein.

As I was reading Filippo’s newsletter, it occurred to me that a dedicated treatment to how cryptographers discuss the Birthday Bound for symmetric encryption would be beneficial.

Birthday Bound?

The Birthday Bound is rooted in the so-called Birthday Paradox in probability theory. It goes something like this:

How many people (chosen from a uniform random distribution) would you need to have in the same room in order for there to be a 50% or greater chance that two of them have the same birthday?

Even though there are 366 possible calendar days in the year (365 if you ignore leap years), the answer is only 23.

This observation can tell us something interesting about the collision risk in discrete uniformly random samples.

For example, the random number (called an IV in this case) used to encrypt a message with AES-CBC, which is a 128-bit random number. This means that there are $2^{128}$ possible values. We can simply describe this situation for any $2^{n}$ distribution; in this case, $n = 128$ .

For any random distribution (i.e., random nonces or tweaks for an AEAD scheme) of $2^{n}$ possible values, you expect to have a 50% chance of collision after about $2^{n/2}$ queries. This is a loose, order-of-magnitude estimate.

From our earlier AES-CBC example, this means $2^{64}$ blocks of data, we’d expect a 50% chance of the two to collide.

My symmetric wear-out blog post went in-depth about the particulars for specific designs, if you’d like to know how the numbers play out.

Is 50/50 Good Enough?

A security policy that cuts off at a 50% chance of a nonce reuse is not fit for the real world. We would call that a YOLO security policy.

AES-GCM, which accepts a 96-bit nonce, is considered unsafe to use for more than $2^{32}$ random nonces. At this point, the probability of a collision for each subsequent message is greater than or equal to $2^{-32}$ .

Consequently, many people consider the point that the risk exceeds $2^{-32}$ the Birthday Bound for a block cipher mode; after which, a new encryption key must be used.

I certainly don’t fault any security policy that keeps the risk of a bad outcome below the $2^{-32}$ mark, but I think there’s another way to interpret what NIST did with AES-GCM. Namely, the fact that GCM’s risk of $2^{-r}$ is exceeded after $2^{r}$ samples (for some fixed value $r$ ) offers a nice symmetry to the risk analysis.

Three Birthday Bounds

(I was originally trying to find a wordplay that references the children’s story Six-Dinner Sid for this section, but ran out of steam and pressed publish before finding an appropriate parody.)
Soatok Editorial Note

This gives rise to three different possible values for a given random distribution that can be considered whenever someone says the phrase “birthday bound”.

50% collision risk after $2^{n/2}$ samples, which I like to think of as the
Hard Birthday Bound.
$2^{-32}$ collision risk after $2^{(n-32)/2}$ samples, which I like to call the
Soft Birthday Bound.
$2^{-r}$ collision risk after $2^{r}$ samples, which I like to call the
Optimal Birthday Bound.

(These labels are not official; a better naming convention may be worth considering, should this framework for discussion prove useful at all.)

Since we’re still dealing with approximations, a useful technique for calculating $r$ is to just take the cube-root of $2^{n}$ (a.k.a., divide the exponent by 3).

In the case of AES-GCM, the Soft and Optimal values are equivalent.

In the case of Filippo’s XAES-256-GCM design? They differ quite a bit.

Whereas the Soft and Optimal limits for a 96-bit nonce are the same, with a 192-bit nonce, they differ a lot: Soft is about 65,536 times the size as Optimal.

Does Any Of This Matter?

If your accepted risk is hard-coded at $2^{-32}$ , then you don’t need to pass Go or collect $200, because your security policy saves you the headache of having to care about math nerd stuff.

However, I do think that the Optimal Birthday Bound is more useful for risk analysis for one simple reason: This is the point at which the probability of a collision is inversely proportional to the number of samples.

Being able to say, “Encrypting $2^{64}$ messages under the same key incurs a probability of a nonce collision of approximately 1 in $2^{64}$ ,” is much more deeply satisfying than arbitrarily focusing on $2^{-32}$ as an arbitrary safety limit.

Of course, to most people, $2^{-32}$ and $2^{-64}$ are both ridiculously small numbers that they “might as well be zero”.

Whenever designing extended-nonce constructions atop AEAD block cipher modes, it may be worthwhile to discuss both the Soft and Optimal limits for nonce collisions.

So long as the people designing extended-nonce constructions at least consider doing this, my work here is done.

Can we get a useful table?

Of course!

Generally, you don’t want to consider a probability space smaller than $2^{96}$ (which is the inflection point where Optimal becomes larger than Soft).

2^{64} — The collision probability for any Optimal Bound is 1 divided by the number of messages.

2^{32} — The collision probability for any Optimal Bound is 1 divided by the number of messages.

Probability Space	Hard Bound	Soft Bound	Optimal Bound
$2^{64}$	$2^{32}$	$2^{16}$	$2^{21.33}$
$2^{96}$	$2^{48}$	$2^{32}$	$2^{32}$
$2^{128}$	$2^{64}$	$2^{48}$	$2^{42.67}$
$2^{160}$	$2^{80}$	$2^{64}$	$2^{53.33}$
$2^{192}$	$2^{96}$	$2^{80}$	$2^{64}$
$2^{224}$	$2^{112}$	$2^{96}$	$2^{74.67}$
$2^{256}$	$2^{128}$	$2^{112}$	$2^{85.33}$
$2^{320}$	$2^{160}$	$2^{144}$	$2^{106.67}$
$2^{384}$	$2^{192}$	$2^{176}$	$2^{128}$
$2^{448}$	$2^{224}$	$2^{208}$	$2^{149.33}$
$2^{512}$	$2^{256}$	$2^{240}$	$2^{170.67}$

To use this table, select a probability space from the left column. Then, on the same row, find the cell corresponding to the type of bound you are interested in.

文章来源: https://soatok.blog/2024/07/01/blowing-out-the-candles-on-the-birthday-bound/
如有侵权请联系:admin#unsafe.sh