Table of Links

Abstract and 1. Introduction

2. Two problems with the current approach to class-incremental continual learning

3. Methods and 3.1. Infinite dSprites

3.2. Disentangled learning

4. Related work

4.1. Continual learning and 4.2. Benchmarking continual learning

5. Experiments

5.1. Regularization methods and 5.2. Replay-based methods

5.3. Do we need equivariance?

5.4. One-shot generalization and 5.5. Open-set classification

5.6. Online vs. offline

Conclusion, Acknowledgments and References

Supplementary Material

5.4. One-shot generalization

To evaluate whether the learned regression network can generalize to unseen classes, we perform a one-shot learning experiment. Here, the model had to normalize and classify transformed versions of shapes it had not previously encountered.

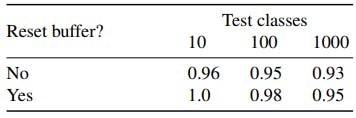
Since the returned class label depends on the exemplars in the buffer, we consider two variants of the experiment, corresponding to generalized and standard one-shot learning. In the first one, we keep the training exemplars in the buffer and add new ones. In the second, the buffer is cleared before including novel exemplars. We also introduce different numbers of test classes. The classification accuracies are presented in Table 1. As expected, keeping the training exemplars in the buffer and adding more test classes makes the task harder. Nevertheless, the accuracy stays remarkably high, showing that the equivariant network has learned a correct and universal mechanism that works even for previously unseen shapes. This is the essence of our framework.

5.5. Open-set classification

Next, we investigate how well our proposed framework can detect novel shapes. This differs from the one-shot generalization task because we do not add the exemplars corresponding to the novel shapes to the buffer. Instead of modifying the learning setup, we use a simple heuristic based on an empirical observation that our model can almost perfectly normalize any input—we classify the input image as unseen if we can’t find an exemplar that matches the normalized input significantly better than others.