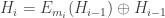
2024-9-2 00:55:1 Author: modexp.wordpress.com(查看原文) 阅读量:17 收藏
Introduction
Constructing your own hash algorithm is controversial because there will always be adversaries that know more about cryptography and can easily break them. I’m not encouraging anyone to construct a cryptographic hash algorithm without extensive knowledge on how to break them first. But in the case of non-cryptographic applications like simple hashing of short strings for trivial purposes, it doesn’t require in-depth cryptanalysis.
Some years ago, I attempted to construct a hash algorithm from block ciphers strictly for the purpose of hashing API strings and nothing more. I was very clear about the intended purpose in a post discussing it. Needless to say, it was initially unsuccessful. It was broken straight away and I received a lot of criticism for writing it. 😀 There was no positive feedback at all. No advice on how to fix any problem that arose: Just ridicule and mockery.
After some corrections, that algorithm was eventually used in a shellcode generator called Donut. I called it Maru (Ma-roo). It uses a Davies-Meyer construction, bit padding (ISO/IEC 9797-1) and SPECK as the block cipher. Although it was clearly not intended for cryptographic purposes, some people chose to ignore that.
Why was the shellcode generator called Donut? Benny/29A published a virus in 2002 he called DotNET. The late Péter Ször who worked at Symantec decided to call it Donut.
Constructions
It’s tempting to use a block cipher with a hash construction but not all ciphers are suitable, so if you’re not a cryptographer and need a cryptographic hash, constructing one this way isn’t advisable. But we’re only interested in hashing API strings, so it doesn’t apply to us. 🙂
1. Davies–Meyer

Feeds each block of the message () as the key to a block cipher. Feeds the previous hash value (
) as the plaintext to be encrypted. The output ciphertext is then also XORed with the previous hash value (
) to produce the next hash value (
). In the first round when there is no previous hash value it uses a constant pre-specified initial value (
).
2. Matyas–Meyer–Oseas

Feeds each block of the message () as the plaintext to be encrypted. The output ciphertext is then also XORed with the same message block (
) to produce the next hash value (
). The previous hash value (
) is fed as the key to the block cipher. In the first round when there is no previous hash value it uses a constant pre-specified initial value (
).
3. Miyaguchi–Preneel

Feeds each block of the message () as the plaintext to be encrypted. The output ciphertext is then XORed with the same message block (
) and then also XORed with the previous hash value (
) to produce the next hash value (
). The previous hash value (
) is fed as the key to the block cipher. In the first round when there is no previous hash value it uses a constant pre-specified initial value (
).
Maru4
The following is pretty much the same as what’s used in Donut. The cipher remains SPECK, except with a 256-bit key and 128-bit block. The rounds for SPECK have been reduced from the official published. Instead of 34 rounds, there’s 4 for each 256-bit block and 12 for the final block. It also doesn’t limit the length of input but it is only intended for short strings.
//
// Maru4 128-bit Hash
// Uses SPECK-128/256 as the permutation function.
//
// Shouldn't be used as a cryptographic hash.
// Use SHA3 for that or something better.
//
#include <stdint.h>
#define ROR64(v, n) (((v) >> (n)) | ((v) << (64 - (n))))
typedef union _w128_t {
uint8_t b[16];
uint32_t w[4];
uint64_t q[2];
} w128_t;
typedef union _w256_t {
uint8_t b[32];
uint32_t w[8];
uint64_t q[4];
} w256_t;
void
encrypt(int rounds, w256_t *key, w128_t *x) {
w256_t k;
k.q[0] = key->q[0];
k.q[1] = key->q[1];
k.q[2] = key->q[2];
k.q[3] = key->q[3];
for (int i=0; i<rounds; i++) {
x->q[1] = (ROR64(x->q[1], 8) + x->q[0]) ^ k.q[0];
x->q[0] = ROR64(x->q[0], 61) ^ x->q[1];
uint64_t t = k.q[3];
k.q[3] = (ROR64(k.q[1], 8) + k.q[0]) ^ i;
k.q[0] = ROR64(k.q[0], 61) ^ k.q[3];
k.q[1] = k.q[2];
k.q[2] = t;
}
}
void
maru4(
const void *input,
const size_t inlen,
const uint64_t seed,
void *output)
{
w128_t hash = {0}, *out=(w128_t*)output;
w256_t tmp={0}, *block = (w256_t*)input;
size_t q = inlen >> 5, r = inlen & 31;
hash.q[0] = seed;
// process 256-bit blocks
for (size_t i = 0; i < q; i++) {
encrypt(4, block, &hash);
block++;
}
// process remaining
for (size_t i = 0; i < r; i++) {
tmp.b[i] = block->b[i];
}
// add padding
tmp.b[r] = 0x80;
// encrypt
encrypt(12, &tmp, &hash);
// return hash
out->q[0] = hash.q[0];
out->q[1] = hash.q[1];
}
Testing Your Hash
If you want to play around with designing your own hash functions, SMHasher can be used to expose common problems associated with poor designs.
Conclusion
There’s nothing wrong with researching and implementing your own hash algorithm so long as it doesn’t find itself in an application that requires a high level of security. But even when you clearly state your design is intended for non-cryptographic purposes, be prepared to have it attacked by the cryptographic community regardless.
如有侵权请联系:admin#unsafe.sh