Table of Links

Abstract and Introduction

Vehicle Modeling

The Nonlinear Feedback Control

OD Corridors and Desired Orientations

Boundary and Safety Controllers

Simulation Results

Conclusion

Appendix A: Collision Detection

Appendix B: Transformed ISO-Distance curves

Appendix C: Local Density

Appendix D: Safety Controller Details

Appendix E: Controller Parameters

References

II. VEHICLE MODELING

A. Vehicle Dynamics

The kinematic bicycle model, that has been extensively used in the literature [11], [12], [36], is employed in this study to represent vehicle dynamics. The model variables are visualized in Fig. 2, and the state-space model reads [11]:

B. Transformation for Circular Movement

While rotating at a roundabout, it is advantageous to transform the above vehicle dynamics to polar coordinates to ease analysis and controller design. Assuming the centre of the roundabout as the origin of the Cartesian and polar coordinates, three new state variables in polar coordinates are defined as below, while the fourth one, i.e. speed, remains unchanged:

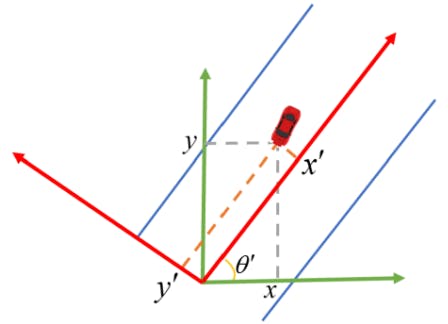
C. Transformation for Skewed Path

D. Sampled-data Bicycle Model

To be implemented in practical frameworks, like simulators, the bicycle model needs to be discretized. Rather than using approximate discretization approaches, like Euler method, the exact sampled-data model is obtained through integrating (1) while considering constant value for control signals during a sampling period. The resulting discrete-time model is [37]:

where k = 0, 1, 2, … is the discrete-time index, and T is the sampling period. For the polar model (5), exact integration appears difficult; hence, we use (8) in the simulation of vehicle dynamics on both straight and circular roads; while the controllers are designed for them based on the respective continuous-time models.

Collision avoidance is the most important goal of control strategies; hence, it is necessary, while simulating vehicle movement, to detect possible collisions among vehicles. Appendix A presents a collision detection procedure for rectangular vehicles.