Deductive Verification of Chain-of-Thought Reasoning in LLMs

Large Language Models (LLMs) significantly benefit from Chain-of-Thought (CoT) prompting in performing various reasoning tasks. While CoT allows models to produce more comprehensive reasoning processes, its emphasis on intermediate reasoning steps can inadvertently introduce hallucinations and accumulated errors, thereby limiting models’ ability to solve complex reasoning tasks. Inspired by how humans engage in careful and meticulous deductive logical reasoning processes to solve tasks, we seek to enable language models to perform explicit and rigorous deductive reasoning, and also ensure the trustworthiness of their reasoning process through self-verification. However, directly verifying the validity of an entire deductive reasoning process is challenging, even with advanced models like ChatGPT. In light of this, we propose to decompose a reasoning verification process into a series of step-by-step subprocesses, each only receiving their necessary context and premises. To facilitate this procedure, we propose Natural Program, a natural language-based deductive reasoning format. Our approach enables models to generate precise reasoning steps where subsequent steps are more rigorously grounded on prior steps. It also empowers language models to carry out reasoning self-verification in a step-by-step manner. By integrating this verification process into each deductive reasoning stage, we significantly enhance the rigor and trustfulness of generated reasoning steps. Along this process, we also improve the answer correctness on complex reasoning tasks. Code will be released at https://github.com/lz1oceani/verify_cot.

1 Introduction

The transformative power of large language models, enhanced by Chain-of-Thought (CoT) prompting [50, 21, 59, 42], has significantly reshaped the landscape of information processing [14, 26, 49, 56, 13, 55, 23, 29], fostering enhanced abilities across a myriad of disciplines and sectors. While CoT allows models to produce more comprehensive reasoning processes, its emphasis on intermediate reasoning steps can inadvertently introduce hallucinations [4, 30, 16, 20] and accumulated errors [4, 51, 1], thereby limiting models’ ability to produce cogent reasoning processes.

In fact, the pursuit of reliable reasoning is not a contemporary novelty; indeed, it is an intellectual endeavor that traces its roots back to the time of Aristotle’s ancient Greece. Motivated by the desire to establish a rigorous reasoning process, in his “Organon,” Aristotle introduced principles of logic, in particular, syllogism, a form of logical argument that applies deductive reasoning to arrive at a conclusion based on two or more propositions assumed to be true. In disciplines that rigorous reasoning is critical, such as judical reasoning and mathematical problem solving, documents must be written in a formal language with a logical structure to ensure the validity of the reasoning process.

We yearn for this sequence of reliable knowledge when answering questions. Our goal is to develop language models that can propose potential solutions through reasoning in logical structures. Simultaneously, we aim to establish a verifier capable of accurately assessing the validity of these reasoning processes. Despite recent significant explorations in the field, such as [48]’s emphasis on self-consistency and [27, 5]’s innovative use of codes to represent the reasoning process, these approaches still exhibit considerable limitations. For example, consistency and reliability are not inherently correlated; as for program codes, they are not powerful enough to represent many kinds of reasoning process, e.g., in the presence of quantifiers (“for all”, “if there exists”) or nuances of natural language (moral reasoning, “likely”, . . . ).

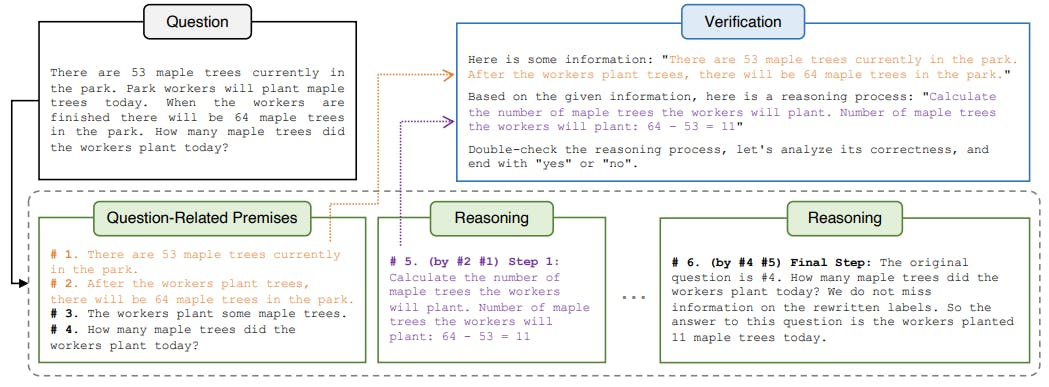
We propose leveraging the power of natural language to achieve the deductive reasoning emphasized in ancient Greek logic, introducing a “natural program”. This involves retaining natural language for its inherent power and avoiding the need for extensive retraining with large data sets. A natural program represents a rigorous reasoning sequence, akin to a computer program. We expect implementations of the idea to have two properties: 1) that natural programs are generated with minimal effort from an existing language model capable of CoT reasoning, preferably through in-context learning; 2) that the natural program can be easily verified for reliability in the reasoning process.

Through a step-by-step investigation, we discovered that large language models have the potential to meet our expectation. Naïve CoT prompts like "Let us think step by step." has many flaws, and entrusting the entire verification process to a large model like ChatGPT can still lead to significant error rates. However, we found that, if the reasoning process is very short, and only based on necessary premises and contexts, the verification of existing large language models is already quite reliable. Therefore, our approach is to design prompts that induce CoT processes comprised of rigorous premises/conditions and conclusions with statement labels, and verification can be done by gradually isolating very few statements within the long thought chain. Experimentally, we found that most reasoning that passed the verification was rigorous, and many that did not pass had elements of imprecision in the reasoning process, even if they occasionally arrived at correct answers.

It is worth emphasizing that, we are not looking for a method to just maximize the correctness rate of final answers; instead, we aspire to generate a cogent reasoning process, which is more aligned with the spirit of judical reasoning. When combined with sampling-based methods, our method can identify low-probability but rigorous reasoning processes. When repeated sampling fails to yield a rigorous reasoning process, we can output "unknown" to prevent hallucinations that mislead users.

We demonstrate the efficacy of our natural program-based verification approach across a range of arithmetic and common-sense datasets on publicly available models like OpenAI’s GPT-3.5-turbo. Our key contributions are as follows:

We propose a novel framework for rigorous deductive reasoning by introducing a “Natural Program” format (Fig. 1), which is suitable for verification and can be generated by just in-context learning;
We show that reliable self-verification of long deductive reasoning processes written in our Natural Program format can be achieved through step-by-step subprocesses that only cover necessary context and premises;
Experimentally, we demonstrate the superiority of our framework in improving the rigor, trustworthiness, and interpretability of LLM-generated reasoning steps and answers (Fig. 2).

文章来源: https://hackernoon.com/deductive-verification-of-chain-of-thought-reasoning-in-llms?source=rss
如有侵权请联系:admin#unsafe.sh