Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
7. Path Encoding in the Adaptive Merkle Tree
The integration of adaptive Merkle Trees into existing blockchain systems like Ethereum presents a paradigm shift in data integrity verification. This shift, while promising significant efficiency gains, also necessitates substantial modifications to current protocols. In Ethereum's existing structure, an account's address directly determines its encoding path in the Patricia-Merkle Tree. This encoding, defined by a series of nibbles (four-bit blocks), uniquely maps each address from the root to a specific leaf in the vast tree structure. The current system's design allows for the seamless integration of new addresses into this expansive tree.
Adopting an adaptive approach fundamentally alters this scenario. Instead of a balanced structure, we would deal with a highly unbalanced tree where frequently used leaves are positioned closer to the root, and less probable leaves are relegated to lower levels. Implementing this directly in the existing Patricia-Merkle Tree structure is not feasible. However, creating a new tree during a protocol update in Ethereum could allow for the incorporation of this adaptive approach, radically changing the concept of path encoding in the tree.
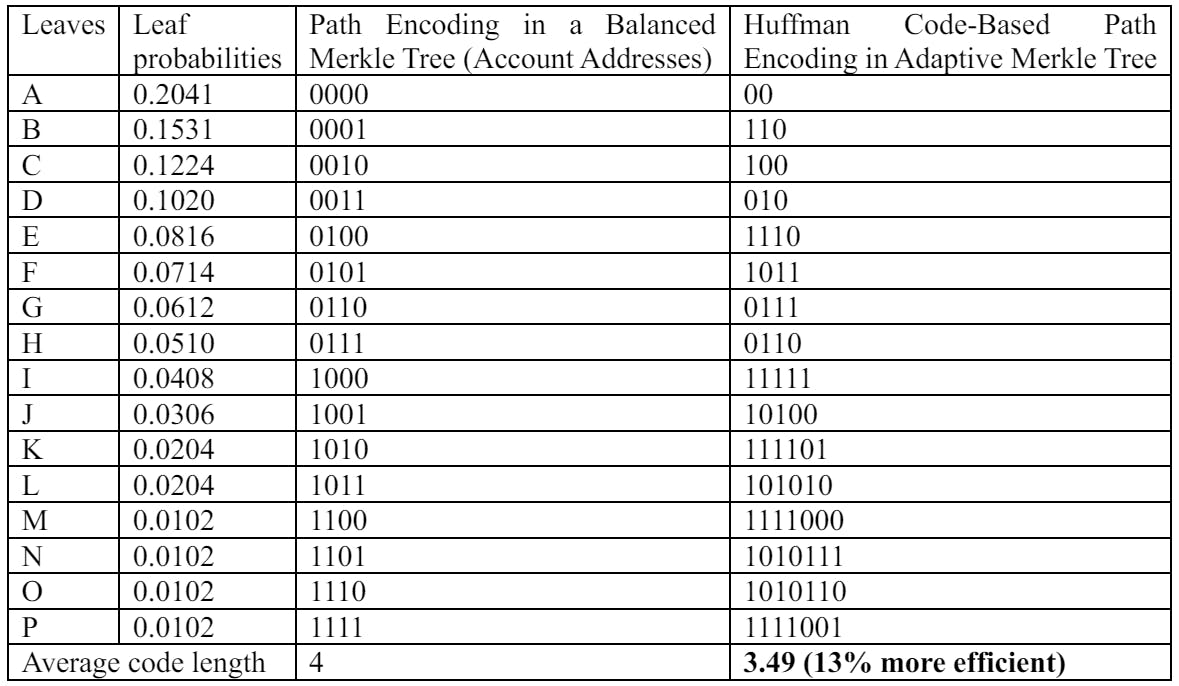
The challenge arises in reconciling existing addresses with new path encodings. In the new structure, a random address would no longer be tied to a specific path encoding but would merely determine the leaf's value, not its path from the root. This concept is illustrated in Figures 34 and 35, where Figure 34 shows the simplified path encoding in a balanced tree with corresponding addresses, and Figure 35 depicts these addresses in an adaptive tree with Huffman code-based path encodings.
A practical solution to address compatibility issues in the adaptive tree is the tabular storage of two structures: "account address – path encoding." This approach allows for the adaptation of the tree based on the usage probabilities of addresses, leading to significant savings in verification complexity and cost. Simultaneously, it preserves the existing mechanism for generating random addresses, including the ability to transfer funds to not-yet-created accounts.


Figure 34 illustrates the path encoding mechanism within a traditional balanced Merkle Tree, as utilized in current blockchain systems like Ethereum. Each account address is directly linked to a unique path encoded by a series of nibbles, efficiently mapping the journey from the tree's root to the respective leaf. This representation underscores the systematic and predictable nature of path encoding in a balanced tree structure, highlighting the ease with which new addresses can be integrated into the expansive tree.
Figure 35 depicts the transformative approach of an adaptive Merkle Tree, where path encodings are based on Huffman codes. This figure contrasts sharply with Figure 34, showcasing a more dynamic and usage-frequency-oriented structure. In this adaptive model, the path encoding is no longer a straightforward derivative of the account address but is instead determined by the frequency of data access, leading to a highly unbalanced but efficient tree structure. This figure effectively demonstrates the shift from a uniform to a tailored approach in path encoding, aligning more closely with the actual usage patterns within the blockchain network.

Table 6 presents a crucial solution to the challenge posed by the transition to an adaptive Merkle Tree: a tabular representation of the correlation between account addresses and their new path encodings. This table exemplifies the practical approach to reconciling the existing system of address generation with the innovative path encoding mechanism of the adaptive tree. By maintaining a record of these correlations, the table ensures that the integrity and functionality of the blockchain are preserved, even as the system evolves to embrace more efficient data verification methods. This tabular approach symbolizes a bridge between the legacy structures of blockchain and the future-oriented adaptive Merkle Tree, ensuring a seamless transition and operational continuity.
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
如有侵权请联系:admin#unsafe.sh