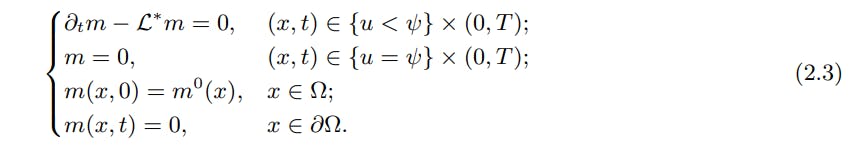
2024-9-25 22:0:28 Author: hackernoon.com(查看原文) 阅读量:1 收藏
Authors:
(1) Chengfeng Shen, School of Mathematical Sciences, Peking University, Beijing;
(2) Yifan Luo, School of Mathematical Sciences, Peking University, Beijing;
(3) Zhennan Zhou, Beijing International Center for Mathematical Research, Peking University.
Table of Links
2 Model and 2.1 Optimal Stopping and Obstacle Problem
2.2 Mean Field Games with Optimal Stopping
2.3 Pure Strategy Equilibrium for OSMFG
2.4 Mixed Strategy Equilibrium for OSMFG
3 Algorithm Construction and 3.1 Fictitious Play
3.2 Convergence of Fictitious Play to Mixed Strategy Equilibrium
3.3 Algorithm Based on Fictitious Play
4 Numerical Experiments and 4.1 A Non-local OSMFG Example
5 Conclusion, Acknowledgement, and References
2.3 Pure Strategy Equilibrium for OSMFG
As for pure strategy equilibrium, we require in addition that all agents choose the same control when they have multiple optimal controls. This is the simplest notion of equilibrium. Now we construct the pure strategy equilibrium in detail.
Suppose that all agents apply the same optimal control, i.e. exit when (x, t) ∈ {u = ψ} and stay when (x, t) ∈ {u < ψ}, the actual crowd propagation will satisfy the following Fokker-Planck equation:

When the actual crowd propagation matches the guessed one (i.e. m = µ), we can combine (2.2) and (2.3) to obtain the PDE system of the Nash equilibrium with pure strategy:

We have mentioned that in some regions of the set {u = ψ}, agents are indifferent between exiting the game and staying in the game. And we have required all agents to leave in such cases. In other words, when an agent faces choices that bring the same cost, they should all choose a specific control rather than individually make a random choice. Therefore, we refer to (2.4) as the pure strategy equilibrium of mean field games with optimal stopping.
However, the pure strategy equilibrium may not exist for mean field game models. In fact, we have the following result:
Theorem 2.1 There exists f and ψ such that there is no solution for (2.4).
We refer to [5] for the proof of such a non-existence result for the stationary case. The construction of f and ψ for the time-dependent case (2.4) is similar and we omit the details here. Instead of elaborating on the proof, we provide an economic intuition for such non-existence.
Consider a game with a population of agents facing an optimal stopping problem, where agents experience crowd aversion. As we will show, there exists no pure strategy Nash equilibrium in this setting. Suppose all other agents follow the pure strategy of exiting at time t. For any individual agent, the cost of staying past t will be low due to crowd aversion. Thus, the agent’s best response is to deviate from the crowd and continue playing. On the other hand, if all agents use the pure strategy of staying past t, an individual agent will prefer exiting at t to avoid the crowd. In either case, no single pure strategy can be sustained in equilibrium, as agents have an incentive to deviate.
The underlying issue is that the definition of pure strategy equilibrium requires all agents to make exactly the same decision, even when indifferent. If we relax this and allow some agents to exit at t while others stay, or have agents randomize between the two actions, an equilibrium may exist. This leads to the concept of mixed strategy equilibrium, where agents follow randomized policies that make opponents indifferent across actions. By permitting randomization, mixed equilibria can capture stable outcomes in games without pure strategy solutions. This provides an avenue to model strategic interactions in mean field games with crowd aversion and optimal stopping.
如有侵权请联系:admin#unsafe.sh