Table of Links

Abstract and 1. Introduction

2 Model and 2.1 Optimal Stopping and Obstacle Problem

2.2 Mean Field Games with Optimal Stopping

2.3 Pure Strategy Equilibrium for OSMFG

2.4 Mixed Strategy Equilibrium for OSMFG

3 Algorithm Construction and 3.1 Fictitious Play

3.2 Convergence of Fictitious Play to Mixed Strategy Equilibrium

3.3 Algorithm Based on Fictitious Play

3.4 Numerical Analysis

4 Numerical Experiments and 4.1 A Non-local OSMFG Example

4.2 A Local OSMFG Example

5 Conclusion, Acknowledgement, and References

4.2 A Local OSMFG Example

Setup. In this example, the state of the representative agent belongs to the same domain as the previous one. The state’s law of motion follows the following SDE:

The initial distribution is a sum of two Gaussian functions:

The running cost f(x, t, m) is defined as

and the stopping cost is defined as

We have used the first-order upwind scheme to discretize the drift term. Other settings are identical to the previous example.

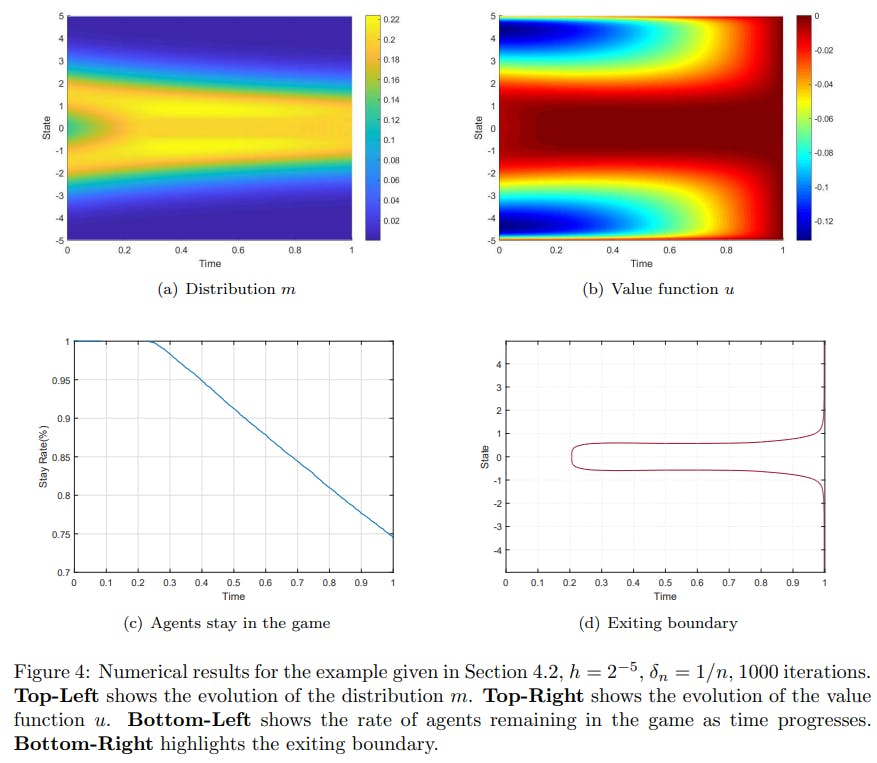
In this example, the dynamics drive the agent to concentrate near the origin. However, the agent dislikes crowded states, and an excessively crowded state would cause an agent to quit. On the other hand, if too many agents quit at a certain state, the running cost becomes attractive again at that location. Therefore, in this example, there doesn’t seem to exist a pure strategy equilibrium.

It can be observed that no agents quit initially, and as more agents gather around x = 0, some begin to quit at around t = 0.25. It is worth pointing out that, unlike the previous example, agents do not quit with 100% certainty upon reaching the exiting boundary in this case. This is evidenced by the fact that the density remains positive for the exiting region. This clearly demonstrates that our solution is a mixed strategy equilibrium.