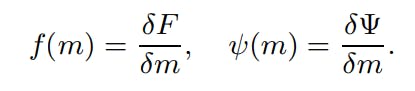
2024-9-26 01:0:24 Author: hackernoon.com(查看原文) 阅读量:1 收藏
Authors:
(1) Chengfeng Shen, School of Mathematical Sciences, Peking University, Beijing;
(2) Yifan Luo, School of Mathematical Sciences, Peking University, Beijing;
(3) Zhennan Zhou, Beijing International Center for Mathematical Research, Peking University.
Table of Links
2 Model and 2.1 Optimal Stopping and Obstacle Problem
2.2 Mean Field Games with Optimal Stopping
2.3 Pure Strategy Equilibrium for OSMFG
2.4 Mixed Strategy Equilibrium for OSMFG
3 Algorithm Construction and 3.1 Fictitious Play
3.2 Convergence of Fictitious Play to Mixed Strategy Equilibrium
3.3 Algorithm Based on Fictitious Play
4 Numerical Experiments and 4.1 A Non-local OSMFG Example
5 Conclusion, Acknowledgement, and References
3.2 Convergence of Fictitious Play to Mixed Strategy Equilibrium
To prove the convergence of the generalized fictitious play (3.1), we first need to ensure that the iteration scheme is well-defined. We introduce the following definition:

Additionally, we require some additional technical assumptions on the functions f and ψ. A common assumption is that f and ψ are variations of potential functions. Games that satisfy this property are known as potential games, of which we present the formal definition as follows.
Definition 3.3 (potential games) We call an optimal stopping mean field game a potential game if there exist potential functions F, Ψ : C → R such that

Now we present the main convergence result. Without loss of generality, we assume the generator of the diffusion process is simply the Laplacian operator ∆ in the subsequent analysis.



From step 1 we know that

Therefore, we have

We define that


By the learning rate condition (3.3), which we recall here for convenience

we can choose N such that

Hence, for all n ≥ M, we have the following inequality:

This is a contradiction with the continuity of Φ and the assumption that m∗ is a cluster point. Thus the cluster point m∗ should satisfy

for all m ∈ T.
3. We conclude that any cluster point (u ∗, m∗) is a mixed strategy equilibrium in this step. We first verify that u ∗ will satisfy the obstacle problem as following:

It remains to verify

and

Define m∗∗ as in (3.13). By (3.21) and the relation

we know that

From (3.11) and (3.12), this equality implies (3.23) and (3.24).
Hence we have finished the proof.
如有侵权请联系:admin#unsafe.sh