In this post, we are having a quick look at a relatively novel protection techniques found in the wild. The class we are looking at is com.X (SHA256: a519e4a20586807665d82ea28892e2ede184807868552f23210bf10c05727980).

Have a look at the decompiled code, with standard JEB options. It was auto-deobfuscated and thoroughly cleaned by dexdec, JEB’s Dalvik decompiler:

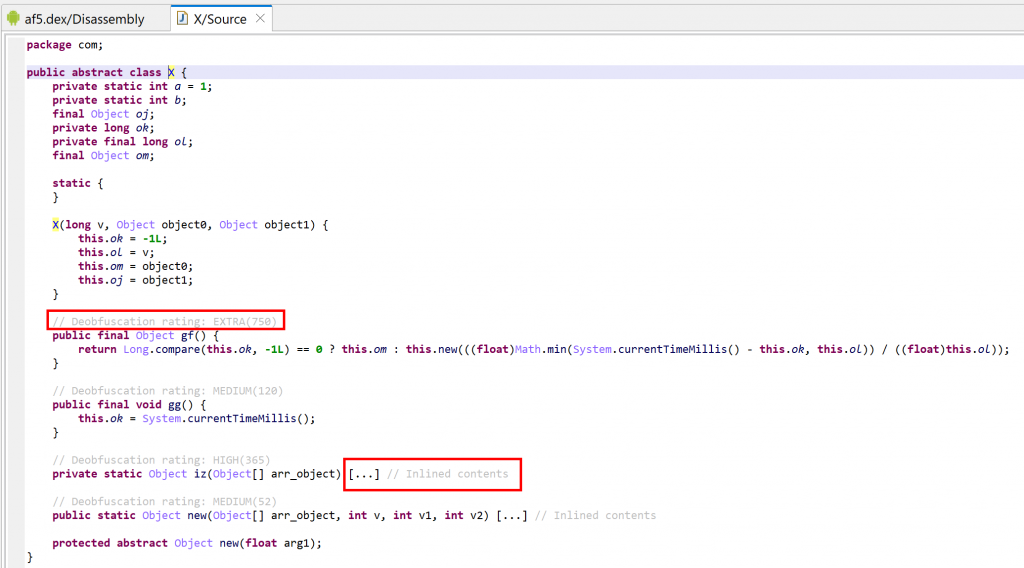
A note on deobfuscation ratings

Two items to notice:

• Some methods outputs are collapsed: their direct output was deemed useless because their code were inlined in corresponding callers. You may re-expand them with the Dash (-) action key, or via the Action menu, Collapse/Expand command.
• Some decompiled methods have an auto-comment specifying a deobfuscation rating and score. This score is calculated from the result of IR optimizers tagged as DEOBFUSCATOR. If the score reaches a threshold, the rating (LOW – not shown-, MEDIUM, HIGH, EXTRA) is specified in the decompilation output, to give a hint to the user that the low-level code is protected, and that the high-level decomp was deobfuscated and cleaned.

The deobfuscation ratings for several methods of com.X are high. It looks like this class received a significant amount of protection. However, after clean-up, the meaningful code consists of two one-liner methods: one storing a timestamp (method gg), the other one calculating an elapsed time (method gf).

Let’s have a look at the decompiled code with deobfuscators disabled: Redecompile the code with CMD1+TAB (Action menu, Decompile with Options…), and untick “Enable deobfuscator optimizers”.

The re-decompilation result is as follows:

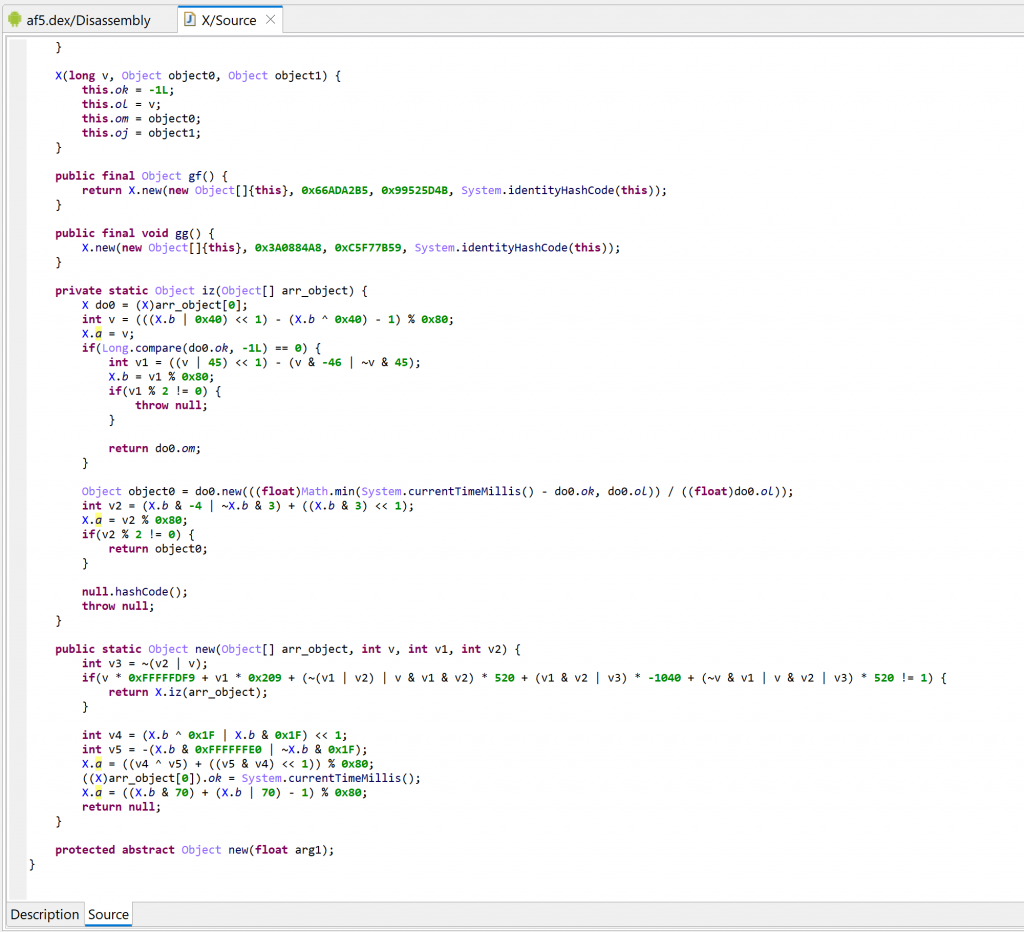
There is quite a lot to look at here, mainly, the fat routines and the opaque predicates.

Inlining “fat” functions

We see that gf calls new with a set of fixed integer (v, v1) as well as the identityHashCode of itself (v3, essentially a pseudo-random number). Similarly, gg also redirects to new, with a different set of arguments.

A quick examination of new shows that two code paths may be executed, based on the values of the provided triplet (v, v1, v2):

So, what happened? The protection of class com.X consisted of taking the bodies of code of gf and gg, merge them into a single method new (hence the name “fat”), and change the codes of gf and gg to trampoline into new with selectors to execute the proper code.

Here is an easier representation of that process, with a single selector (instead of a triplet):

// UNPROTECTED CLASS C
class C 
  int fld1;
  
  int f1(int x) {
    return 25 + x;
  }
  
  int f2() {
    return 31 * fld1;
  }
}

// PROTECTED CLASS C
class protected_C
  int fld1;

  int f1(int x) {
    return (int)fat_routine(new Object[]{this, x}, 1);
  }
  
  int f2() {
    return (int)fat_routine(new Object[]{this}, 2);
  }
  
  static Object fat_routine(Object[] params, int selector) {
    if(selector == 1) {
      return 25 + (int)params[1];
    }
    else if(selector == 2) {
      return 31 * ((C)params[0]).fld1;
    }
    throw new RuntimeException();  // should not happen
  }
}

Although the above code is trivial, we can use it to highlights two complications the decompiler will face when dealing with the more complex implementations made by the a real code protection system:

• When to decide to inline, i.e. how to detect fat functions? (that question is outside the scope of this blog, and would not be of much interest to most readers)
• What about complex selectors, such as a triplet with a pseudo-random int?

If JEB’s dexdec were to inline the calls to new as it is, we’d end up with the following decomps – not quite what we saw at the beginning of this article!

Resolving opaque predicates

Let’s look at method gf. We can see that the pseudo-random selector, after inlining, is used to calculate a predicate that will determine which path to take, i.e. do we execute the actual code for gf, or the code for gg?

The predicate seen in gf can be re-written as:

PRED = 0xDE9B00B0 + (~(0x99525D4B | X) | 1 & X) * 520 + (0x99525D4B & X | ~(X | 0x66ADA2B5)) * -1040 + (0x99525D4A | 0x66ADA2B5 & X | ~(X | 0x66ADA2B5)) * 520 != 1

Internally, JEB does quite a bit to simplify it, and ultimately, when all fast reductions and simplifications are applied, it will use the well-known Z3 SMT solver to break the predicate. In this case, regardless of the value of X, the predicate is true. Therefore, gf will be simplified to:

return X.iz(arr_object);

(Note that method iz is itself a candidate for inlining! At the end, the cleaned-up code shown in the introduction of this article will be generated.)

The use of Z3 and other external theorem provers that may be used by JEB and its plugins can be disabled in the option (see “Enable predicate breaker”):

Conclusion

We hope this quick note will shed some light on some newer features or recent upgrades that went into dexdec. Many of those were already present in gendec, the generic decompiler used for anything non-Dalvik, and it was about time to add those advanced clean-up passes into the Dalvik decompiler as well. In a sense, dexdec has caught up and even gone further than gendec on these aspects.

Which leads me to say there will likely be a Part 2 or at least an update for this blog, to highlight another complex deobfuscating task: the simplification of arithmetic operations consisting of bitwise operations and mixed boolean/arithmetic (MBA) expressions.

Stay tuned! Thank you to all our users and readers of this blog 🙂 Do not hesitate to reach out through the usual channels (Slack, email, X).

– Nicolas