Table of Links

Abstract and Introduction

SALSA- (S)ubstitution, (A)pproximation, Evo(L)utionary (S)earch, and (A)B-Initio Calculations

SALSA Applied to Photocatalytic Water-splitting

Discussion

Methods

Conclusions, Data Availability Statement and References

Appendix: Supplementary Material

V. METHODS

A. Initial Dataset

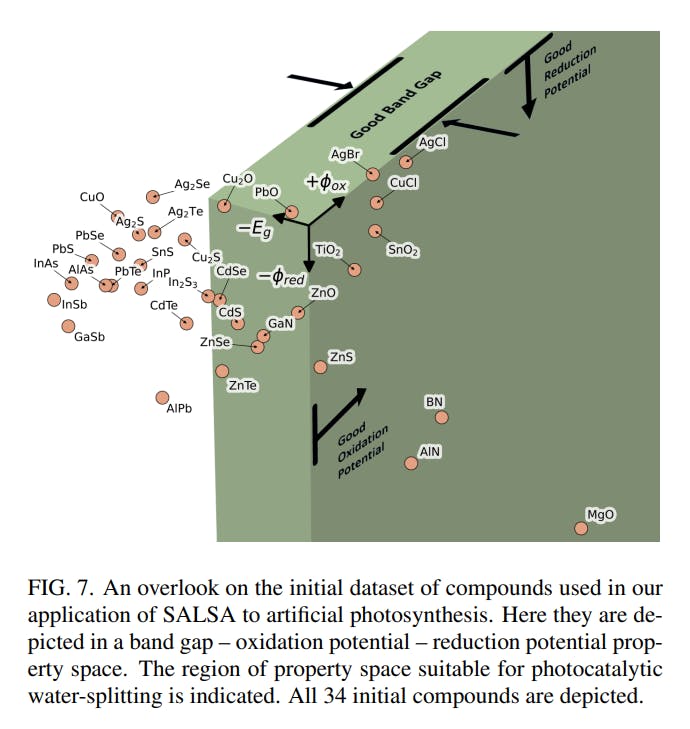
We first collected a dataset of experimentally determined semiconductor band gaps. We then applied the method described in Stafford et al. 2023c in prep to calculate reduction and oxidation potentials. This formed an initial dataset containing 34 compounds. We sought compounds with band gaps between 1.23–2.80 eV to enable efficient photoabsorption. We also sought reduction potentials below 0.00 V and oxidation potentials above 1.23 V, with respect to the NHE, for materials which are stable in an aqueous environment. None of our original materials had suitable values for all three properties. Figure 7 presents an overview of the collection of initial compounds and the region of property space described above. Table IV lists each initial compound, its band gap and its redox potentials.

Figure 8 in the Supplementary Material presents a closer look at the swarm of compounds that hover just outside of the target space. Few compounds are stable to photo-catalyzed decomposition. This is mainly because most have oxidation potentials that are too low, leaving them prone to hole oxidation (Figure 8 (d)). However, some of the few with acceptable oxidation potentials have reduction potentials that are too high (Figure 8 (b)). Additionally, compounds are roughly evenly divided into three groups which cannot absorb sunlight efficiently, cannot absorb it at all in the regions of higher solar intensity, and which have an acceptable band gap (Figure 8 (e) and (c)). No matter which angle we look at this property space, we see there is great room for improvement.

B. Parameters Used for Candidate Generation

a. Substitution Threshold We used a substitution threshold of 0, that is, we did not consider substitutions associated with negative values in our substitution likelihood matrix. This parameter can be adjusted as governed by the computational resources available to a search. A lower threshold enables a more thorough exploration of composition space, but is more computationally expensive and less efficient at finding suitable materials.

b. Substitution Implementation We allowed substitution to constitute a complete or partial replacement of the original ion. For example, Br− ↔ I − is a matrix-allowed substitution and AgBr is in our initial dataset so compounds of the form AgnBrn –m Im with n,m ∈ Z, are in our candidate dataset. We limited substitutions to be first or second order, i.e at most two substitutions could be used to generate an individual candidate. In Section III, first and second-order substitutions correspond to ternary and quaternary compounds, respectively. Theoretically, a second-order substitution could consist of exchanging a single, original ionic component for two new ions. However, second-order substitutions that formed hybrid compounds consisted of a single substitution of each of the original components as this is the only way a secondorder substitution could correspond to interpolation between two binary compounds. Building on the previous example, the substitution Ag+ ↔ Cu+ could be used in second-order substitutions to produce quaternary compounds of the form Agn – pCupBrn –m Im with n, p,m ∈ Z. For the purpose of enumerating a complete dataset, the new components of candidate compounds were limited to half or less the final composition. So all second-order substitutions were partial and you could not generate CuI (n = p = m = 1) from just AgBr. However, this limitation does not affect hybrid compounds.

c. Unit Cell Size Limit In practice, the enumeration of candidate compounds requires some constraint on values of n,m, p. Results presented in Section III implemented this constraint by imposing a maximum of 20 atoms in a unit cell. This is equivalent to the constraints 1 ≤ n, p,m ≤ 10 in the previous example.

C. Property Space Selection Criteria

With our interpolation scheme we filtered compounds that did not meet the following criteria: 1.03 < band gap (eV) < 3.00, oxidation potential (V) > 1.03, and reduction potential (V) < 0.2. This includes an extra window of 0.20 eV for the band gaps and 0.20 V for the potentials to allow for materials that might ultimately arrive in the desired region of property space by deviating slightly from their linear interpolation. To illustrate this process, consider PbSe and CuCl. PbSe’s band gap is too small, at 0.27 eV, and its oxidation potential is too low, at 0.76 eV, while CuCl has too high a band gap at 3.40 eV. However, the 50:50 interpolation between these two, PbCuSeCl, has band gap, oxidation and reduction potentials of 1.84 eV, 1.23 V and −0.25 V, respectively, which places it just inside the threshold of our target region.

D. Interpolation

We construct hybrid compositions which are integer ratios of two parent compositions. We then estimate the properties of the corresponding hybrid compounds to be linear interpolations of the parent compounds on a per-atom basis. In other words, we weight the initial property values by the number of atoms contributed to the hybrid. Furthermore, we don’t restrict our interpolations to be single-substitution. For example, both Pb2+ ↔ Cu+ and Se2− ↔ Cl− are matrixallowed substitutions so if we start with initial compounds PbSe and CuCl, we generate interpolated compositions such as PbCuSeCl.

E. USPEX Settings

We provide USPEX a composition and allow it to perform all stochastic modifications it has at its disposal. We do not constrain the structure by space group. For energy evaluation, we elect USPEX’s option to interface with the DFT code, Vienna Ab initio Simulation Package (VASP).32–34 All VASP calculations were performed in the plane-wave DFT framework at the Generalized Gradient Approximation (GGA) level of theory and used the Perdew, Burke, and Ernzerhof (PBE) functional.35 Projector-augmented wave (PAW) pseudopotentials were used to represent the core electrons and ion-electron interactions.36,37 We used a plane-wave cutoff of 500 eV, an energy convergence criterion of 10−4 eV, and force convergence of 0.02 eV/A. Dispersive interactions were ac- ˚ counted for using DFT-D3 corrections38 with Becke-Jonson damping.39 We also included spin polarization effects.

F. CRYSTAL17 Settings