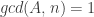
Shellcode: Obfuscation with Permutations

Shellcode: Obfuscation with Permutations
2024-10-19 01:15:4 Author: modexp.wordpress.com(查看原文) 阅读量:6 收藏

Introduction
Affine Transformation
Linear Congruential Generator (LCG)
Inversive Congruential Generator (ICG)
Modular Multiplication
Affine Permutation
References

Appendix

Affine Cipher
Affine Hash
Modular Involutions

1. Introduction

In a previous post on masking, shuffling data was suggested as an alternative to encryption or compression that generates high-entropy data. A block cipher in Counter (CTR) mode along with the Fisher-Yates shuffle was used, which, in hindsight, was a bit excessive. Herm1t proposed using a Linear Congruential Generator (LCG) for shuffling and an Inversive Congruential Generator (ICG) for unshuffling, which helped reduce the amount of code. Others tried implementing shuffling ideas here and here, but did not address the issue of random access. After some further reading about LCGs and their applications, this led to Affine Permutations simply because the formula is exactly the same as what’s used for generating random numbers, hash algorithms and classical encryption. Permutations rearrange objects which makes them ideal for masking data. They are reversible and suitable for scrambling or obfuscating the order of elements without losing information.

2. Affine Transformation

If you’re a programmer or reverse engineer, you’ll no doubt have encountered code that combines a multiplication, addition and division one after the other. Even some architectures like ARM64 have a dedicated Multiply-add instruction (MADD) and a Multiply-subtract instruction (MSUB) to increase performance of Matrix multiplication, audio processing, graphics processing and modular arithmetic used in classical, elliptic curve and post-quantum cryptography. The following is how to express an Affine Transformation in the context of linear algebra and geometry:

$f(x) = A \times x + b$

$\text{where:}$

When used with a finite set of integers modulo $n$ , a transformation is bijective if the scaling factor $A$ is coprime with the modulus $n$ . i.e. $gcd(A, n)=1$ . This ensures that multiplication by $A$ is invertible modulo $n$ , making the transformation one-to-one. The translation term $b$ shifts the output but doesn’t affect the bijectivity

$f(x) = A \times x + b \mod n$

Affine permutations are bijective functions when the scaling factor and modulus are coprime, ensuring that every element is unique.
Cryptography often relies on bijections to ensure that data can be encoded and decoded without loss of information.

3. Linear Congruential Generator (LCG)

There’s a strong similarity between an Affine Transformation and LCG invented by W. E. Thomson and published in a 1958 work titled A Modified Congruence Method of Generating Pseudo-random Numbers. The LCG is a widely known method for generating pseudo-random numbers, particularly for non-cryptographic applications.

$X_{0} = seed$

$X_{n+1} = (a \cdot X_n + c) \mod m$

$\text{where:}$

The seed is initialised with something like the current time X-D. It’s not random, but if you’re using an LCG for cryptographic purposes, using the time as a seed is the least of your problems. An implementation in C might look like the following:

// LCG parameters based on RtlUniform in Windows
static uint64_t X = 1;
static uint64_t a = ((int)(0x80000000 - 19)); // 2**31 - 19
static uint64_t c = ((int)(0x80000000 - 61)); // 2**31 - 61
static uint64_t m = ((int)(0x80000000 - 1));  // 2**31 - 1

set_seed(uint64_t seed) {
    X = seed;
}

uint64_t 
lcg() {
    X = (a * X + c) % m;
    return X;
}

N.B. In affine transformations, $A$ is used for the scaling factor, $b$ for the translation (shift) term and $n$ for any modulus. In the case of an LCG, the multiplier $a$ is equivalent to $A$ , the increment $c$ corresponds to the translation term $b$ , and the modulus $m$ serves the same purpose as the term $n$ . The terminology differs, but both processes describe an affine-like transformation of the sequence. I found the inconsistency in notation to be confusing at first, but obviously affine transformations were studied in geometry and linear algebra long before computing. LCGs are primarily used in number theory and pseudorandom number generation hence the differences in notation. In the case of Affine Permutation, I will use the same notation used to describe an LCG, which could be wrong. Let me know in the comment section.

4. Inversive Congruential Generator (ICG)

The concept was proposed by Jürgen Eichenauer and Jürgen Lehn in their 1986 paper titled A Non-Linear Congruential Pseudo Random Number Generator. They argued these were more effective at generating random numbers than LCGs.

$X_{n+1} = \left( a \cdot X_n^{-1} + c \right) \mod m$

$\text{where:}$

Herm1t also discussed this in a 2011 paper titled Inversing Random Numbers which appeared in Virus Writing Bulletin #1. (since archive.org is down as of writing this on October 17th 2024, I can’t link to the article right now, but will update later.)

The C code here is based on details provided by Herm1t. It’s using 64-bit integers instead of 32-bit because of integer overflows that occur with prime numbers like $2^{31-1}$ . Oddly enough, composite numbers like $2^{32}$ work fine with 32-bit integers.

int64_t 
invmod(int64_t a, int64_t m) {
    int64_t m0 = m, t, q;
    int64_t x0 = 0, x1 = 1;

    if (m == 1)
        return 0;

    while (a > 1) {
        q = a / m;
        t = m;
        m = a % m;
        a = t;
        t = x0;
        x0 = x1 - q * x0;
        x1 = t;
    }

    if (x1 < 0)
        x1 += m0;

    return x1;
}

We compute the multiplicative inverse modulo $m$ for the multiplier $a$ and increment $c$ .

    a = invmod(a, m);
    c = -c * a;

And now the inversive generator can run in reverse.

uint64_t 
icg() {
    uint64_t tmp = X;
    X = (a * X + c) % m;
    return tmp;
}

If we run both lcg() and icg() a number of times, we get the following results:

LCG output...
lcg(1) : 40C97C31
lcg(2) : 71D54448
lcg(3) : 7F0132A3
lcg(4) : 11EA703C
lcg(5) : 3D841B89

ICG output...
icg(1) : 3D841B89
icg(2) : 11EA703C
icg(3) : 7F0132A3
icg(4) : 71D54448
icg(5) : 40C97C31

Source of more complete example here.

The following function provided by herm1t allows us to skip numbers in forward and reverse which partially solves the problem of random access. There’s a similar solution provided in an article titled Random Number Generation with Arbitrary Stride.

// http://number-none.com/blow/blog/programming/2016/07/08/fabian-on-lcg-fast-forward.html
uint64_t 
skip(uint32_t X, uint64_t a, uint64_t c, unsigned n) {
    while (n) {
        if (n & 1)
            X = a * X + c;
        c *= a + 1;
        a *= a;
        n >>= 1;
    }
    return X;
}

5. Modular Multiplication

The ShiftRows step in AES is described as a “cyclic permutation” because it rotates the bytes in each row of the state matrix by a certain number of positions in a circular fashion. This operation effectively permutes the positions of the bytes within each row, enhancing the diffusion property of the cipher. I’ve seen it implemented in various ways and it’s typically like the following:

// taken from https://github.com/ilvn/aes256
void aes_shiftRows(uint8_t *buf)
{
    register uint8_t i, j; /* to make it potentially parallelable :) */

    i = buf[1]; 
    buf[1] = buf[5]; 
    buf[5] = buf[9]; 
    buf[9] = buf[13]; 
    buf[13] = i;
    
    i = buf[10]; 
    buf[10] = buf[2]; 
    buf[2] = i;
    
    j = buf[3]; 
    buf[3] = buf[15]; 
    buf[15] = buf[11]; 
    buf[11] = buf[7]; 
    buf[7] = j;
    
    j = buf[14]; 
    buf[14] = buf[6]; 
    buf[6] = j;

} /* aes_shiftRows */

This works fast on most architectures. Another way (less efficient) might be implemented like the following:

void ShiftRows(uint8_t state[4][4], int Nb, uint8_t shifted[4][4]) {
    for (int r = 0; r < 4; r++) {
        for (int c = 0; c < Nb; c++) {
            int new_col = (c + shift(r, Nb)) % Nb;
            shifted[r][c] = state[r][new_col];
        }
    }
}

Based on the first example, you can see it’s swapping elements in the state matrix. The indices are:

$\text{Permuted Index: } \{0,\ 5,\ 10,\ 15,\ 4,\ 9,\ 14,\ 3,\ 8,\ 13,\ 2,\ 7,\ 12,\ 1,\ 6,\ 11\}$

It’s possible to use modular multiplication to generate these indices on the fly which requires much less code to compute. Permuted Indices can be generated with:

$f(i) = (5 \times i) \mod 16$

$f(i)$ refers to the permuted index for the $i$ -th iteration of the loop.

// permuted indices
for (int i=0; i<16; i++) {
    printf("%ld, ", (5 * i) % 16);
}

$\text{Inverse Permuted Index: } \{0,\ 13,\ 10,\ 7,\ 4,\ 1,\ 14,\ 11,\ 8,\ 5,\ 2,\ 15,\ 12,\ 9,\ 6,\ 3\}$

$f(i) = (13 \times i) \mod 16$

$f(i)$ refers to the inverse permuted index for the $i$ -th iteration of the loop.

// inverse permuted indices
for (int i=0; i<16; i++) {
    printf("%ld, ", (13 * i) % 16);
}

To understand the relationship between 5 and 13, the following table lists coprimes of 16 and the multiplicative inverse modulo 16. For ShiftRows, numbers 5 and 11 can be used to generate permuted indices, while 3 and 13 can generate inverse permuted indices with modular addition, subtraction or multiplication. 1 does nothing. 15 can be used to reverse the elements. 7 and 9 are self-inverse “modular involutions” unrelated to ShiftRows.

Number $a$	Inverse $a^{-1}$
1	1
3	11
5	13
7	7
9	9
11	3
13	5
15	15

It was LargeCardinal pointed out to me how to create the inverse permuted indices using an iterative loop:

$X_{i+1} = (X_i - 3) \mod 16$

    uint32_t X, i;
    
    for (X = i = 0; i < 16; i++) {
        X = (X - 3) % 16;
    }

You can generate the same indices with addition in a loop or multiplication using 13. It’s possible with right-to-left iteration too.

If you want to use modular multiplication to permute a set of elements, the following works well:

$f(i) = (a \times i) \mod m$

$\text{where:}$

When $a$ and $m$ are coprime, the sequence will have a maximal period of $[0, m - 1]$ , covering all possible indices without repetition. It’s very much like a Multiplicative LCG (MLCG) because $c$ is zero. But the parameters selected are different.

6. Affine Permutation

Modular multiplication, as used in AES’s ShiftRows operation, can be an effective method for permuting elements of an array. However, not all multipliers result in full permutations over the set of elements, which can lead to repeating patterns or incomplete coverage of the array. For example, with a modulus of 16, using a multiplier of 1 leaves the array unchanged, while using 15 simply reverses it. Even if the multiplier is coprime with the modulus, this alone may not generate a sufficiently randomized or evenly distributed permutation. Introducing an offset, shift, or increment (similar to the technique used in LCGs) can enhance the randomness of the generated indices, resulting in a better distribution of elements.

$f(i) = (a \times i + c) \mod m$

$\text{where:}$

When $a$ and $m$ are coprime, the sequence will have a maximal period of $[0, m - 1]$ , covering all possible indices without repetition. It’s very similar to an LCG, which is why some have called it a single iteration of LCG or Linear Congruential Permutation (LCP). To demonstrate how it works visually.

In the following example, we use $a=3, c=5, m=16$ but you can update this with your own values.

import numpy as np

# Affine function to permute indices
def affine_perm(a, c, m):
    return [(a * i + c) % m for i in range(m)]

# Parameters
a = 3  # Multiplier
c = 5  # Shift
m = 16 # Modulus

# m-byte array (indices from 0 to m-1)
array = np.arange(m)

# Permute indices
permuted_indices = affine_perm(a, c, m)

# Use the permuted indices to create a permuted array
permuted = array[permuted_indices]

# Print the original and permuted arrays
print("\n")
print("Original array:     ", array)
print("Permuted array:     ", permuted)

When you run this:

Original array:      [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
Permuted array:      [ 5  8 11 14  1  4  7 10 13  0  3  6  9 12 15  2]

Python source to demonstrate encoding and decoding of files.

7. References

Appendix

Apart from random number generators and permutation algorithms, affine functions can also be used for simple ciphers and hash functions. Non-cryptographic hash functions are very useful for a variety of computer applications.

2. Affine Cipher

The origin and first use of the term Affine Cipher remains unclear. A contributor to Stack Exchange found references to it in cryptography books from 1983 and 1995, but earlier uses are difficult to pinpoint. Since common Linear Algebra terms like “function,” “mapping,” and “transformation” are often used interchangeably, adding “cipher” or “hashing” clarifies the specific cryptographic intent of the affine function. The Affine Cipher can be likened to a single iteration of a LCG for encryption, while decryption resembles a single iteration of an ICG.

Encryption:

$E(x) = (a \times x + b) \mod m$

Decryption:

$D(y) = a^{-1} \times (y - b) \mod m$

where:

It goes without saying that this cipher is highly insecure and should not be used for anything serious. However, it could be useful for a CTF or reverse engineering challenge.

3. Affine Hash

The concept of Universal Hash Functions was introduced by Larry Carter and Mark Wegman in their 1979 paper titled “Universal Classes of Hash Functions“. In this work, they developed a mathematical framework for creating families of hash functions with strong probabilistic guarantees against collisions. This research eventually led to the development of perfect hash functions that I might cover in a later post. I could find at least two types of hash algorithms based on a single iteration of LCG (or at least very similar to that):

As with “transformation” or “mapping”, we see the terms “linear”, “affine” or “multiplicative” when describing these hash algorithms.

3.1 Linear Hash Functions

This is another example of using a single iteration of an LCG, this time to generate a hash. Didn’t investigate what kind of parameters should be used, but imagine they’re similar to ensuring a maximal period or full cycle of the modulus. The concept of “perfect” hash functions is interesting and might be covered in a future post.

$h(k) = (a \cdot k + b) \mod m$

3.2 Multiplicative Hash Functions.

A variation of the previous hash uses an irrational number

$h(k) = \left\lfloor m \times \left( (A \times k) \mod 1 \right) \right\rfloor$

Knuth recommends using the Golden Ratio as $A$ but any irrational number like Euler’s number should work well too.

Golden Ratio

$\text{ 1.618034 } = \phi = \frac{1 + \sqrt{5}}{2}$

In C, you can generate the number using:

double phi = sqrt(5.0) + 1.0) / 2.0;

Euler’s Number

$\text{ 2.718282 } = e^{1}$

In C, you can generate the number using:

double e = exp(1.0);

PI

$\text{ 3.141593 } = \pi = 2.0 \times \arccos(0.0)$

In C, you can generate the number using:

double pi = 2.0 * acos(0.0);

4. Modular Involutions

7 and 9, that are coprimes of 16, can be used with modular multiplication to create an involution: $P(P(i)) = i$

To find involutive multipliers for any modulus:

Identify numbers that are coprime to the modulus
For each coprime number $a$ , check if $a^{2} \mod m = 1$

# Function to find involutive multipliers
def find_invol_mul(m):
    coprimes = []
    # Find numbers coprime with m
    for a in range(2, m - 1):
        if gcd(a, m) == 1:
            coprimes.append(a)

    invol_mul = []
    
    # Check for each coprime if a^2 % m == 1
    for a in coprimes:
        if (a * a) % m == 1:
            invol_mul.append(a)
    
    return invol_mul

If the size of $m$ exceeds 16-bits, this can take a long time and isn’t really practical. Maybe if there was a way to find them faster, then this could be useful for large permutations. I’m not aware of any algorithm.

5. Lehmer Random Number Generator

This was invented by D.H Lehmer in 1948 and published in a 1951 work titled Mathematical Methods in Large-scale Computing Units from Proceedings of a Second Symposium on Large Scale Digital Calculating Machinery; Annals of the Computation Laboratory, Harvard Univ. 26 (1951), pp. 141-146.

$X_{0} = seed$

$X_{k+1} = (a \cdot X_k) \mod m$

$\text{where:}$

文章来源: https://modexp.wordpress.com/2024/10/18/shellcode-obfuscation-with-permutations/
如有侵权请联系:admin#unsafe.sh

Table Of Contents

Appendix

1. Introduction

2. Affine Transformation

3. Linear Congruential Generator (LCG)

4. Inversive Congruential Generator (ICG)

5. Modular Multiplication

6. Affine Permutation

7. References

Appendix

2. Affine Cipher

Encryption:

Decryption:

3. Affine Hash

3.1 Linear Hash Functions

3.2 Multiplicative Hash Functions.

Golden Ratio

Euler’s Number

PI

4. Modular Involutions

5. Lehmer Random Number Generator