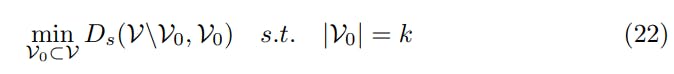
2024-10-22 16:0:18 Author: hackernoon.com(查看原文) 阅读量:3 收藏
Authors:
(1) Junwei Su, Department of Computer Science, the University of Hong Kong and [email protected];
(2) Chuan Wu, Department of Computer Science, the University of Hong Kong and [email protected].
Table of Links
5 A Case Study on Shortest-Path Distance
6 Conclusion and Discussion, and References
9 Procedure for Solving Eq. (6)
10 Additional Experiments Details and Results
11 Other Potential Applications
9 Procedure for Solving Eq. (6)
First recall that the optimization problem we want to solve is as follows.

where k is the given initial set size and Ds(.) is given in Def. 2 with shortest path distance as the metric. Eq. 6 amounts to the well-known k-center problem [14] in graph theory and is NP-hard. For our experiment, we use Eq. 6 as guidance and modify the simple greedy algorithm, farthest-first traversal, to be a sampling method for obtaining a solution. We now describe how we modified the standard greedy algorithm into a sampling algorithm. We start with describing the standard greedy algorithm.

The procedure described above is a standard 2-approximation greedy algorithm for k-center problem. Next, we describe its sampling variant which use the distance as the chance of being sampled.
9.1 Running Time Complexity
It is obvious that the procedure above runs in O(k) if the distance between any pair of vertices is given and runs in O(kn) if the distance needed to be computed for each step, where n is the number of vertice.
如有侵权请联系:admin#unsafe.sh