Table of Links

1. Abstract

2. Introduction

   Background

   Reinforcement Learning

   Similar Work

3. Methodology

   DRLAgent Design

4. Training Procedures

5. Testing Procedures

6. Results

7. SABR Experiments

8. Conclusions

9. Appendix A

10. References

RESULTS

This section presents and discusses the results of numerical experiments. As described in the methodology, a DRL agent is first trained using simulations of a GBM process, and the testing results of this GBM trained agent are presented first. Not only are GBM experiments conducted with and without transaction costs, the robustness of the DRL agent is assessed by conducting an experiment at a volatility level higher than what was seen by the DRL agent in training. Next, the real-world applicability is assessed by testing DRL agents trained with market-calibrated stochastic volatility models, noting that the first stochastic volatility test uses arbitrary parameters.

Geometric Brownian Motion Experiment

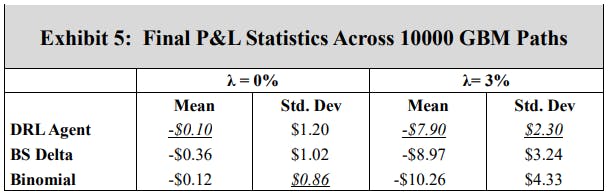
In the first experiment, a DRL agent is trained using GBM asset paths. Exhibits 3 and 4 show the resulting final P&L distributions when the transaction cost rates, λ, are 0 and 3%, respectively. Note that separate subplots are used for ease of comparison, and the DRL agent results are the same when compared to the BS Delta and binomial strategies in each subplot. Exhibit 5 summarizes the mean and standard deviations of the final P&L for DRL, BS Delta, and binomial hedging, and the highest (lowest) mean (standard deviation) is italicized and underlined for each transaction cost rate. Exhibits 6 and 7 show sample hedging actions for one asset path that finishes out of the money (OTM), and one asset path that crosses the early exercise boundary.

A comparison of Exhibits 3 and 4 shows the impact of a cost conscious DRL agent. When there are no transaction costs, the DRL agent hedges effectively, producing a higher mean final P&L than the BS Delta method. This is an expected result, as the BS Delta method does not consider early exercise. However, the DRL agent does not achieve a higher mean final P&L than the binomial strategy, and the standard deviation of final P&L’s is highest for the DRL agent. However, when there are 3% transaction costs, the DRL agent achieves a higher mean final P&L and lower standard deviation than both the BS Delta and binomial strategies. Exhibits 5 and 6 aid in illustrating the DRL agent’s awareness of premature exercise risk while maintaining a focus on transaction costs. At early time steps, the DRL agent hedges similarly to the binomial strategy, and the BS Delta strategy does not consider early exercise and, therefore, has the lowest hedge position. While the three strategies converge when the threat of early exercise decreases and the asset price moves out of the money, as is in the case in Exhibit 6, the DRL agent tends to react more slowly to abrupt price movements. When there is a spike in the required asset position, the DRL agent tends to under-hedge relative to the other two strategies. Likewise, the DRL agent tends to over-hedge when there is a dip in the required asset position. This displays the cost-consciousness of the DRL agent and helps show why the DRL method outperforms the other two strategies when transaction costs are present.

The second GBM experiment aims to display the robustness of the DRL agent. Call to mind that the DRL agent is trained with a volatility of 20%, the binomial strategy is computed with trees constructed with 20% volatility, and the BS Delta strategy uses a volatility of 20% to compute both the option price and Delta. As such, let this 20% volatility be labelled as 𝜎𝑎𝑔𝑒𝑛𝑡. Now consider a scenario wherein GBM asset paths evolve with a volatility of 24%. Moreover, let the option buyer use the correct volatility of 24% to compute an exercise boundary for exercise decisions. As such, this volatility of 24% is given the label 𝜎𝑏𝑢𝑦𝑒𝑟. In this scenario, not only are the hedging agents using an incorrect volatility to hedge the option, but the initial option price is computed with a lower volatility, and the option is therefore sold under value. Exhibits 8 through 10 summarize the results of this volatility experiment.

The results of Exhibits 8 through 10 show that the DRL agent is more robust to an inaccurate volatility estimate than the BS Delta and binomial tree strategies. With no transaction costs, the DRL agent has a higher mean final P&L than the other two strategies, and a lower standard deviation than the binomial strategy. With transaction costs considered, the DRL agent once again outperforms both the BS Delta and the binomial strategies, achieving a higher mean final P&L, as well as a lower standard deviation.

This paper is available on arxiv under CC BY-NC-SA 4.0 Deed (Attribution-Noncommercial-Sharelike 4.0 International) license.