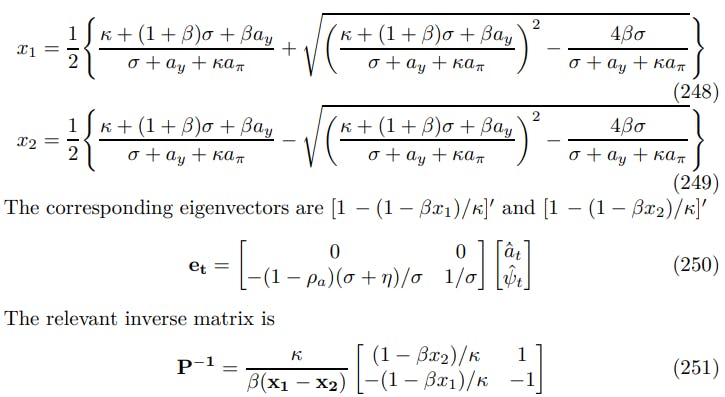
2024-12-11 05:0:12 Author: hackernoon.com(查看原文) 阅读量:2 收藏
Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
C.2 Extending No Persistence
This subsection generalizes lack of persistence in two directions. The first is to show that in the absence of price dispersion, it extends to all approximations from ZINSS. Similar results are well-known for Rotemberg. The second shows that even when the output gap is adjusted to allow technology shocks, inflation still responds to demand shocks only on impact.
C.2.1 Higher Order Dynamics

C.2.2 Dynamics with Unobserved Natural Rate

Although no persistence breaks down, propagation problems still arise, in particular, with respect to inflation and aggregate demand shocks. The destruction of endogenous persistence when shock persistence takes limiting values is a theme common to the whole paper. This analysis has appeared before. The task at hand is to diagonalize (240) and substitute into the forward solution of (239) and then compute the persistence. First solve (241)-(243), this yields

The relevant inverse matrix is

using the forward solution and several rounds of substitution yields the following expression for inflation

Deploying the persistent properties of the errors, communicated in Subsection 4.7, this yields

It is intuitive that a positive supply shock drives down inflation. Away from the two limiting cases where it vanishes, as with Divine Coincidence, there is positive persistence, measured by the product moment correlation coefficient

It is still pathological to Keynesian intuition that inflation does not respond to demand shocks. For output the expression is

Again, the desired limiting cases arise. There can be overshooting or undershooting with respect to the efficient benchmark.110 However, the underlying message is that this system cannot generate persistent responses from inflation to demand shocks.

如有侵权请联系:admin#unsafe.sh